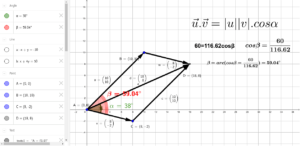
Exploraremos la fórmula para calcular el vector resultante. El vector resultante es la suma de dos o más vectores individuales. Aprenderemos cómo sumar algebraicamente los componentes de los vectores en cada dirección y cómo calcular la magnitud y dirección del vector resultante.
Fórmula general para calcular el vector resultante
La fórmula general para calcular el vector resultante implica sumar algebraicamente los componentes de los vectores en cada dirección. Para vectores bidimensionales, se suman los componentes en la dirección x y en la dirección y por separado. La fórmula es la siguiente:
VR = V1 + V2 + V3 + … + Vn
Donde VR es el vector resultante y V1, V2, V3, … Vn son los vectores individuales que se están sumando. Cada vector individual se descompone en sus componentes en x y en y, y luego se suman algebraicamente.
Por ejemplo, si tenemos dos vectores V1 y V2, con componentes en x y en y, podemos calcular el vector resultante VR de la siguiente manera:
VRx = V1x + V2x
VRy = V1y + V2y
 Rapidez
RapidezLuego, el vector resultante VR se obtiene combinando los componentes en x y en y:
VR = (VRx, VRy)
Fórmula para calcular la magnitud y dirección del vector resultante
En términos de magnitud y dirección, la fórmula para calcular el vector resultante es la siguiente:
VR = √(Vx^2 + Vy^2)
Donde Vx es la suma de los componentes en la dirección x y Vy es la suma de los componentes en la dirección y. La magnitud del vector resultante se obtiene calculando la raíz cuadrada de la suma de los cuadrados de los componentes en cada dirección.
Para calcular la dirección del vector resultante, se utiliza la función tangente inversa:
 Vaporización
Vaporizaciónθ = arctan(Vy/Vx)
Donde θ es el ángulo de dirección del vector resultante. La función tangente inversa se utiliza para encontrar el ángulo cuya tangente es igual a la relación entre los componentes en la dirección y y en la dirección x.
Consideraciones importantes
Es importante tener en cuenta algunas consideraciones al calcular el vector resultante:
– Los vectores deben estar en la misma unidad y en el mismo sistema de coordenadas para poder sumarlos correctamente. Si los vectores están en diferentes unidades o sistemas de coordenadas, es necesario convertirlos antes de sumarlos.
– Se debe tener en cuenta el sentido de cada vector al sumarlos, ya que un cambio en el sentido de un vector puede cambiar el resultado final. Si un vector tiene un sentido contrario al otro, se debe restar en lugar de sumar.
– Es necesario descomponer cada vector en sus componentes en x y en y antes de sumarlos. Esto implica identificar la magnitud y dirección de cada componente en cada dirección.
– La magnitud y dirección del vector resultante se calculan utilizando las fórmulas mencionadas. La magnitud se obtiene calculando la raíz cuadrada de la suma de los cuadrados de los componentes en cada dirección, y la dirección se obtiene utilizando la función tangente inversa.
Ejemplo de cálculo del vector resultante
Para ilustrar cómo se utiliza la fórmula para calcular el vector resultante, consideremos el siguiente ejemplo:
Tenemos dos vectores V1 y V2, con las siguientes componentes:
 Generador
GeneradorV1 = (3, 4)
V2 = (-2, 6)
Para calcular el vector resultante VR, primero sumamos los componentes en cada dirección:
VRx = V1x + V2x = 3 + (-2) = 1
VRy = V1y + V2y = 4 + 6 = 10
Luego, combinamos los componentes en x y en y para obtener el vector resultante VR:
VR = (1, 10)
Para calcular la magnitud del vector resultante, utilizamos la fórmula:
VR = √(Vx^2 + Vy^2) = √(1^2 + 10^2) = √(1 + 100) = √101
Por lo tanto, la magnitud del vector resultante es √101.
Para calcular la dirección del vector resultante, utilizamos la fórmula:
θ = arctan(Vy/Vx) = arctan(10/1) = arctan(10)
Por lo tanto, la dirección del vector resultante es arctan(10).
Conclusión
La fórmula para calcular el vector resultante implica sumar algebraicamente los componentes de los vectores en cada dirección. También se puede calcular la magnitud y dirección del vector resultante utilizando las fórmulas mencionadas. Es importante tener en cuenta el sentido de cada vector y asegurarse de que estén en la misma unidad y sistema de coordenadas antes de sumarlos. Además, es necesario descomponer cada vector en sus componentes en x y en y antes de sumarlos. La magnitud se obtiene calculando la raíz cuadrada de la suma de los cuadrados de los componentes en cada dirección, y la dirección se obtiene utilizando la función tangente inversa.