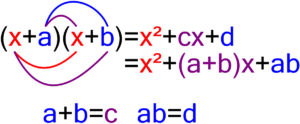La factorización es un proceso matemático que consiste en descomponer una expresión algebraica en factores más simples. Este proceso es utilizado en diferentes ramas de las matemáticas, como el álgebra, la aritmética y la geometría. La factorización es una herramienta importante para resolver ecuaciones, simplificar expresiones y realizar operaciones matemáticas más eficientemente.
Exploraremos los diferentes tipos de factorización, cómo se realiza en cada caso y proporcionaremos ejemplos para ilustrar los conceptos. Comenzaremos por analizar los tipos más comunes de factorización: la factorización de polinomios, la factorización de números enteros y la factorización de matrices.
Tipos de factorización
Existen diferentes tipos de factorización, dependiendo del tipo de expresión que se desea factorizar. Algunos de los tipos más comunes son:
1. Factorización de polinomios
La factorización de polinomios es un proceso que consiste en descomponer un polinomio en el producto de otros polinomios más simples. Esto se realiza encontrando los factores del polinomio original que, al multiplicarse, dan como resultado el polinomio original.
Existen diferentes métodos para realizar la factorización de polinomios, dependiendo de las características del polinomio. Algunos de los métodos más comunes son:
- Factorización por factor común
- Factorización por agrupación
- Factorización por diferencia de cuadrados
- Factorización por trinomio cuadrado perfecto
- Factorización por trinomio de la forma ax^2 + bx + c
2. Factorización de números enteros
La factorización de números enteros consiste en descomponer un número entero en el producto de sus factores primos. Un número primo es aquel que solo tiene dos factores: él mismo y 1. Por lo tanto, la factorización de un número entero implica encontrar los números primos que, al multiplicarse, dan como resultado el número original.
El teorema fundamental de la aritmética establece que todo número entero mayor que 1 puede descomponerse de una única forma en números primos. Esto significa que la factorización de un número entero es única, aunque el orden de los factores puede variar.
Para factorizar un número entero, se pueden seguir los siguientes pasos:
- Dividir el número entre el menor número primo posible. Si el número es divisible por ese primo, se divide y se continúa dividiendo el cociente obtenido hasta que ya no sea divisible por ese primo.
- Repetir el paso anterior con el siguiente número primo, y así sucesivamente, hasta que el cociente obtenido sea igual a 1.
- Los factores primos obtenidos en cada división son los factores primos del número original.
3. Factorización de matrices
La factorización de matrices consiste en descomponer una matriz en el producto de dos o más matrices. Esta descomposición puede ser útil para resolver sistemas de ecuaciones lineales, calcular determinantes o realizar operaciones matriciales más eficientemente.
Existen diferentes métodos de factorización de matrices, dependiendo de las propiedades de la matriz y el objetivo de la factorización. Algunos de los métodos más comunes son:
- Factorización LU
- Factorización QR
- Factorización de Cholesky
Cómo se realiza la factorización
La factorización se realiza siguiendo diferentes métodos y técnicas, dependiendo del tipo de expresión que se desea factorizar. A continuación, se detallan los pasos para realizar la factorización en cada tipo:
1. Factorización de polinomios
Para factorizar un polinomio, se pueden seguir los siguientes métodos:
- Factorización por factor común: Se extrae el factor común que se repite en todos los términos del polinomio y se divide cada término entre ese factor.
- Factorización por agrupación: Se agrupan los términos del polinomio de manera que se pueda factorizar por factor común en cada grupo.
- Factorización por diferencia de cuadrados: Se aplica la fórmula de la diferencia de cuadrados para factorizar un polinomio que es una diferencia de dos cuadrados perfectos.
- Factorización por trinomio cuadrado perfecto: Se aplica la fórmula del trinomio cuadrado perfecto para factorizar un polinomio que puede ser expresado como el cuadrado de un binomio.
- Factorización por trinomio de la forma ax^2 + bx + c: Se busca descomponer el trinomio en dos binomios de la forma (px + q)(rx + s), donde p, q, r y s son coeficientes.
2. Factorización de números enteros
Para factorizar un número entero, se pueden seguir los siguientes pasos:
- Dividir el número entre el menor número primo posible. Si el número es divisible por ese primo, se divide y se continúa dividiendo el cociente obtenido hasta que ya no sea divisible por ese primo.
- Repetir el paso anterior con el siguiente número primo, y así sucesivamente, hasta que el cociente obtenido sea igual a 1.
- Los factores primos obtenidos en cada división son los factores primos del número original.
3. Factorización de matrices
Para factorizar una matriz, se pueden seguir diferentes métodos, dependiendo de las propiedades de la matriz y el objetivo de la factorización. Algunos de los métodos más comunes son:
- Factorización LU: Se descompone la matriz en el producto de una matriz triangular inferior y una matriz triangular superior.
- Factorización QR: Se descompone la matriz en el producto de una matriz ortogonal y una matriz triangular superior.
- Factorización de Cholesky: Se descompone una matriz simétrica y definida positiva en el producto de una matriz triangular inferior y su traspuesta.
Conclusiones
La factorización es un proceso matemático que consiste en descomponer una expresión algebraica en factores más simples. Existen diferentes tipos de factorización, como la factorización de polinomios, la factorización de números enteros y la factorización de matrices. Cada tipo de factorización tiene sus propios métodos y técnicas para realizar la descomposición. La factorización es una herramienta importante en matemáticas y tiene aplicaciones en diferentes áreas, como la resolución de ecuaciones, el cálculo de determinantes y la optimización de operaciones matriciales.