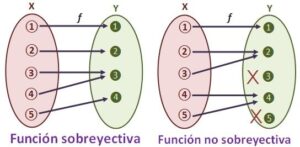
Función Sobreyectiva – Conceptualista

Exploraremos en detalle las propiedades de una función sobreyectiva. Una función sobreyectiva es un tipo de función que tiene características específicas en términos de su codominio, imagen, relación uno a uno, recorrido y dominio. También veremos ejemplos para comprender mejor cómo funcionan las funciones sobreyectivas.

Propiedades de una función sobreyectiva

Codominio

El codominio de una función sobreyectiva es el conjunto de salida, que puede contener muchos valores que no se utilizan en la función. Por ejemplo, si tenemos una función f: A → B, donde A es el conjunto de entrada y B es el conjunto de salida, el codominio sería el conjunto B.

Imagen

La imagen de una función sobreyectiva son los valores del codominio que realmente salen de la función. En otras palabras, son los valores de salida que se obtienen al aplicar la función a los elementos del conjunto de entrada. Por ejemplo, si tenemos una función f: A → B, la imagen sería el conjunto de valores en B que se obtienen al evaluar f(x) para cada x en A.

Relación uno a uno

En una función sobreyectiva, cada elemento del conjunto de salida tiene al menos un elemento del conjunto de entrada al que le corresponde. En términos formales, se puede escribir como f(x) = y, donde a cada y le corresponde una o más x. Esto significa que no hay elementos en el conjunto de salida que no tengan un elemento correspondiente en el conjunto de entrada.

Recorrido y dominio iguales

En una función sobreyectiva, el recorrido (conjunto de salida) y el dominio (conjunto de partida o conjunto de definición) son iguales. Esto significa que todos los elementos del conjunto de salida están siendo utilizados y tienen un elemento correspondiente en el conjunto de entrada.

Función sencilla

Una función sobreyectiva se caracteriza por ser de fácil comprensión y solución. Proporciona un camino directo entre el conjunto de entrada y el conjunto de salida, ya que cada elemento de salida tiene al menos un vínculo con un elemento de entrada. Esto facilita la comprensión y resolución de la función.

Solución directa

Aunque la ecuación en sí puede ser compleja, una función sobreyectiva no nos deja atascados en un paso previo a la solución. Se puede analizar en sentido contrario, desde el conjunto de salida hasta el conjunto de entrada, lo que facilita la resolución. Esto significa que podemos encontrar fácilmente los elementos del conjunto de entrada que corresponden a un elemento dado del conjunto de salida.

Conclusiones

Una función sobreyectiva es aquella en la que cada elemento del conjunto de salida tiene al menos un elemento del conjunto de entrada al que le corresponde. Tiene un recorrido y un dominio iguales, y se caracteriza por ser de fácil comprensión y solución. Las funciones sobreyectivas son útiles en muchos contextos matemáticos y tienen aplicaciones prácticas en diversas áreas.

Ejemplos de funciones sobreyectivas

1. Función lineal: f(x) = 2x + 3, donde el conjunto de entrada es el conjunto de números reales y el conjunto de salida es el conjunto de números reales. Esta función es sobreyectiva porque para cada número real y, podemos encontrar un número real x que cumple f(x) = y.

2. Función exponencial: f(x) = 2^x, donde el conjunto de entrada es el conjunto de números reales y el conjunto de salida es el conjunto de números reales positivos. Esta función es sobreyectiva porque para cada número real positivo y, podemos encontrar un número real x que cumple f(x) = y.