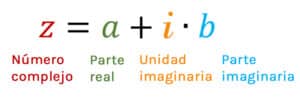Exploraremos en detalle la definición y concepto de los números complejos. Veremos cómo se componen, cómo se representan en un plano complejo y cómo se utilizan en diferentes campos de las matemáticas y la física. También proporcionaremos ejemplos para ayudar a comprender mejor este fascinante conjunto de números.
¿Qué son los números complejos?
Los números complejos son un conjunto de cifras que resultan de la suma entre un número real y uno imaginario. Un número real es aquel que puede ser expresado por un número entero o decimal, mientras que un número imaginario es aquel cuyo cuadrado es negativo.
Parte Real e Imaginaria
Los números complejos están compuestos por una parte real y una parte imaginaria. La parte real se refiere al número real en la suma, mientras que la parte imaginaria se refiere al número imaginario en la suma. La parte imaginaria se representa con la letra «i».
Representación en el Plano Complejo
Los números complejos se representan en un plano complejo, que es un plano bidimensional con un eje real y un eje imaginario. La parte real se representa en el eje horizontal (eje real) y la parte imaginaria se representa en el eje vertical (eje imaginario). Esto permite visualizar los números complejos como puntos en el plano complejo.
El Cuerpo Complejo
Los números complejos forman un cuerpo complejo, lo que significa que cumplen con ciertas propiedades algebraicas. Estas propiedades incluyen la cerradura bajo la suma y la multiplicación, la existencia de un elemento neutro para la suma y la multiplicación, la existencia de inversos aditivos y multiplicativos, y la propiedad distributiva.
Historia de los números complejos
La noción de números complejos surgió debido a la imposibilidad de los números reales de abarcar las raíces de orden par de los números negativos. A lo largo de la historia, matemáticos como Herón de Alejandría y Descartes contribuyeron al desarrollo de los números complejos, pero fue Gauss quien los redescubrió y les dio la atención que merecían.
Aplicaciones de los números complejos
Los números complejos se utilizan en diversos campos de las matemáticas, la física y la ingeniería debido a su capacidad para representar corriente eléctrica y ondas electromagnéticas. Algunas de las aplicaciones más comunes de los números complejos incluyen:
Álgebra Lineal
En álgebra lineal, los números complejos se utilizan para representar matrices y vectores complejos. Esto es especialmente útil en el estudio de sistemas lineales y transformaciones lineales.
Teoría de Circuitos
En la teoría de circuitos eléctricos, los números complejos se utilizan para representar la impedancia de un circuito. Esto permite analizar y resolver problemas relacionados con la corriente eléctrica y la potencia en un circuito.
Análisis de Señales
En el análisis de señales, los números complejos se utilizan para representar señales sinusoidales y ondas electromagnéticas. Esto permite analizar y manipular señales en el dominio de la frecuencia.
Geometría y Trigonometría
En geometría y trigonometría, los números complejos se utilizan para representar puntos en el plano complejo y realizar operaciones como rotaciones y traslaciones. También se utilizan en la representación de coordenadas polares y en la resolución de problemas trigonométricos.
Diagramas de Argand
Para interpretar los números complejos de manera geométrica, se utiliza un plano complejo y se relacionan con vectores y coordenadas polares. Los diagramas de Argand se utilizan para representar las posiciones de los polos y los ceros de una función en el plano complejo.
Conclusiones
Los números complejos son un conjunto de cifras que resultan de la suma entre un número real y uno imaginario. Se utilizan en diversos campos de las matemáticas, la física y la ingeniería debido a su capacidad para representar corriente eléctrica y ondas electromagnéticas. Los números complejos se representan en un plano complejo y forman un cuerpo complejo. Su interpretación geométrica se realiza a través de diagramas de Argand.