Exploraremos en detalle el concepto de paralelepípedo, un cuerpo geométrico con características particulares. Veremos su definición, sus propiedades y ejemplos para comprender mejor este concepto.
Un paralelepípedo es un cuerpo geométrico limitado por seis paralelogramos, con caras opuestas paralelas e iguales. Es un poliedro formado por superficies planas y tiene ocho vértices y doce aristas. Existen diferentes tipos de paralelepípedos, como el cubo, el paralelepípedo oblicuo, el paralelepípedo rectangular y el romboedro. El cálculo de las propiedades de los paralelepípedos, como el volumen, se basa en fórmulas que dependen de las características particulares de la figura.
2. Definición de Paralelepípedo
Un paralelepípedo es un cuerpo geométrico limitado por seis paralelogramos, con caras opuestas paralelas e iguales. Es un poliedro formado por superficies planas y tiene ocho vértices y doce aristas.
2.1 Tipos de Paralelepípedos
Existen diferentes tipos de paralelepípedos, cada uno con características específicas:
- Cubo: un paralelepípedo con todas las caras iguales y ángulos rectos.
- Paralelepípedo oblicuo: un paralelepípedo con caras no perpendiculares entre sí.
- Paralelepípedo rectangular: un paralelepípedo con caras perpendiculares entre sí.
- Romboedro: un paralelepípedo con caras romboidales.
3. Propiedades de los Paralelepípedos
Los paralelepípedos tienen varias propiedades que los distinguen:
- Ángulos: los ángulos internos de un paralelepípedo pueden ser rectos, agudos u obtusos, dependiendo de su forma.
- Caras: un paralelepípedo tiene seis caras, todas ellas paralelogramos.
- Vértices: un paralelepípedo tiene ocho vértices, donde se encuentran las aristas.
- Aristas: un paralelepípedo tiene doce aristas, que son los segmentos de línea donde se encuentran las caras.
- Simetría: un paralelepípedo puede tener diferentes tipos de simetría, dependiendo de su forma y características.
4. Cálculo de Propiedades de los Paralelepípedos
El cálculo de las propiedades de los paralelepípedos, como el volumen y el área de las caras, se basa en fórmulas que dependen de las características particulares de la figura. Estas fórmulas pueden variar según el tipo de paralelepípedo.
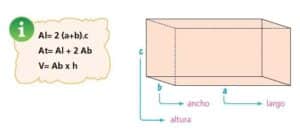
4.1 Fórmula del Volumen
La fórmula general para calcular el volumen de un paralelepípedo es:
Volumen = longitud × anchura × altura
4.2 Fórmula del Área de las Caras
La fórmula general para calcular el área de las caras de un paralelepípedo es:
Área de la cara = longitud × anchura
5. Ejemplos de Paralelepípedos
A continuación, se presentan algunos ejemplos de paralelepípedos:
- Un cubo de Rubik es un ejemplo de un paralelepípedo cuyas caras son todas iguales.
- Un ladrillo es un ejemplo de un paralelepípedo rectangular utilizado en la construcción.
- Un diamante es un ejemplo de un paralelepípedo oblicuo con caras romboidales.
6. Conclusiones
Un paralelepípedo es un cuerpo geométrico formado por seis paralelogramos con caras opuestas paralelas e iguales. Tiene propiedades y características específicas, como ángulos, caras, vértices y aristas. El cálculo de sus propiedades se basa en fórmulas que dependen de su forma particular. Los paralelepípedos se encuentran en diversos objetos y estructuras en nuestra vida cotidiana.