Exploraremos en detalle el concepto de grafos, una estructura fundamental en matemáticas y ciencias de la computación. Aprenderemos qué es un grafo, cómo se representa y las diferentes características que pueden tener. También veremos ejemplos prácticos para comprender mejor su funcionamiento.
Definición de Grafos
Un grafo es un objeto unitario de naturaleza abstracta que abarca a las grafías que componen una letra. En matemáticas y ciencias de la computación, un grafo es una representación gráfica de puntos llamados nodos o vértices, que están conectados por líneas llamadas aristas. Los grafos pueden ser simples o complejos, conexos o fuertemente conexos, completos o bipartitos, dependiendo de sus características. La teoría de los grafos fue desarrollada por Leonhard Euler en el siglo XVIII.
Componentes de un Grafo
Nodos o Vértices
Los nodos o vértices son los puntos individuales en un grafo. Cada nodo puede representar una entidad o un elemento en un conjunto. Por ejemplo, en un grafo que representa una red de transporte, los nodos pueden representar ciudades o estaciones.
Aristas
Las aristas son las líneas que conectan los nodos en un grafo. Representan las relaciones o conexiones entre los elementos representados por los nodos. Las aristas pueden ser dirigidas o no dirigidas, dependiendo de si la relación entre los nodos tiene una dirección específica o no.
Tipos de Grafos
Grafos Simples
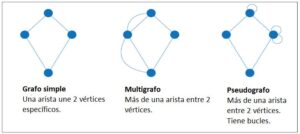
Un grafo simple es aquel en el que no hay aristas múltiples entre los mismos pares de nodos y no hay bucles, es decir, aristas que conectan un nodo consigo mismo.
Grafos Complejos
Un grafo complejo es aquel en el que puede haber aristas múltiples entre los mismos pares de nodos y/o bucles.
Grafos Conexos
Un grafo conexo es aquel en el que hay un camino entre cualquier par de nodos. En otras palabras, no hay nodos aislados en el grafo.
Grafos Fuertemente Conexos
Un grafo fuertemente conexo es aquel en el que hay un camino dirigido entre cualquier par de nodos. En este tipo de grafo, se puede llegar de cualquier nodo a cualquier otro nodo siguiendo las aristas en la dirección correcta.
Grafos Completos
Un grafo completo es aquel en el que hay una arista entre todos los pares de nodos. En otras palabras, todos los nodos están conectados directamente entre sí.
Grafos Bipartitos
Un grafo bipartito es aquel en el que los nodos se pueden dividir en dos conjuntos disjuntos, de manera que todas las aristas conecten nodos de un conjunto con nodos del otro conjunto, pero no haya aristas que conecten nodos dentro del mismo conjunto.
Aplicaciones de los Grafos
Los grafos tienen una amplia gama de aplicaciones en diversos campos, incluyendo:
- Redes de transporte y logística
- Redes sociales y análisis de redes
- Algoritmos de búsqueda y rutas óptimas
- Análisis de dependencias y relaciones en bases de datos
- Modelado de sistemas complejos
Ejemplos de Grafos
Para comprender mejor cómo se ven y cómo funcionan los grafos, veamos algunos ejemplos prácticos:
Ejemplo 1: Red de Transporte
Imaginemos una red de transporte con ciudades como nodos y carreteras como aristas. Cada ciudad estaría conectada a otras ciudades a través de las carreteras. Este grafo sería un ejemplo de un grafo no dirigido y conexo.
Ejemplo 2: Red Social
En una red social, los usuarios pueden ser representados como nodos y las conexiones entre ellos (amistades, seguidores, etc.) como aristas. Este grafo sería un ejemplo de un grafo no dirigido y posiblemente bipartito si hay diferentes tipos de usuarios (por ejemplo, amigos y seguidores).
Ejemplo 3: Mapa de Rutas Aéreas
En un mapa de rutas aéreas, los aeropuertos pueden ser representados como nodos y los vuelos entre ellos como aristas. Este grafo sería un ejemplo de un grafo dirigido y posiblemente completo si hay vuelos directos entre todos los aeropuertos.
Conclusiones
Los grafos son una herramienta poderosa para representar y analizar relaciones y conexiones entre elementos. Su estudio y aplicación en matemáticas y ciencias de la computación ha llevado al desarrollo de numerosos algoritmos y técnicas que se utilizan en una amplia variedad de campos. Esperamos que este artículo haya proporcionado una comprensión clara y completa de los grafos y sus diferentes características.