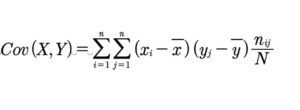Exploraremos en detalle el concepto de covarianza. Veremos qué es la covarianza, cómo se calcula y qué información nos proporciona sobre la relación entre dos variables aleatorias. También discutiremos algunas propiedades importantes de la covarianza y proporcionaremos ejemplos para una mejor comprensión.
¿Qué es la covarianza?
La covarianza es un valor que indica cómo varían dos variables aleatorias en conjunto con respecto a sus medias. Nos permite entender cómo se comporta una variable en relación con otra. La covarianza puede ser positiva, negativa o cero, dependiendo de la relación entre las variables.
Cálculo de la covarianza
La covarianza se calcula utilizando la siguiente fórmula:
cov(X, Y) = Σ((X – μX)(Y – μY)) / n
Donde:
- cov(X, Y) es la covarianza entre las variables X e Y.
- X e Y son las variables aleatorias.
- μX y μY son las medias de X e Y, respectivamente.
- n es el número de observaciones.
La fórmula de la covarianza se basa en la diferencia entre cada observación de X y su media, multiplicada por la diferencia entre cada observación de Y y su media. Estos productos se suman y se dividen por el número de observaciones.
Propiedades de la covarianza
La covarianza tiene varias propiedades importantes que debemos tener en cuenta:
Covarianza cero
La covarianza es cero cuando una de las variables es una constante. Esto significa que si una de las variables no varía en absoluto, no hay relación entre las dos variables y la covarianza es cero.
Covarianza y varianza
La covarianza entre una variable y sí misma es igual a la varianza de esa variable. Esto se debe a que la covarianza mide cómo una variable varía en relación con otra, y si la otra variable es la misma, entonces estamos midiendo cómo una variable varía en relación consigo misma, lo cual es igual a su varianza.
Simetría
La covarianza es simétrica en el orden de las variables. Esto significa que la covarianza entre X e Y es igual a la covarianza entre Y y X. La simetría de la covarianza nos permite intercambiar el orden de las variables sin afectar el resultado.
Interpretación de la covarianza
La covarianza nos proporciona información sobre la relación entre dos variables aleatorias. Dependiendo del valor de la covarianza, podemos interpretar diferentes tipos de relaciones:
Covarianza positiva
Si la covarianza es positiva, esto indica que las variables tienden a moverse en la misma dirección. En otras palabras, cuando una variable aumenta, la otra variable también tiende a aumentar. Esto sugiere una relación positiva entre las variables.
Covarianza negativa
Si la covarianza es negativa, esto indica que las variables tienden a moverse en direcciones opuestas. En otras palabras, cuando una variable aumenta, la otra variable tiende a disminuir. Esto sugiere una relación negativa entre las variables.
Covarianza cero
Si la covarianza es cero, esto indica que no hay una relación lineal entre las variables. Esto no significa necesariamente que no haya ninguna relación entre las variables, solo que no hay una relación lineal.
Ejemplos de covarianza
Para ilustrar mejor el concepto de covarianza, veamos algunos ejemplos:
Ejemplo 1: Altura y peso
Supongamos que tenemos una muestra de personas y queremos analizar la relación entre su altura y peso. Calculamos la covarianza entre estas dos variables y obtenemos un valor positivo. Esto indica que, en general, a medida que la altura de una persona aumenta, su peso también tiende a aumentar. Sin embargo, la covarianza no nos dice nada sobre la fuerza o la dirección exacta de la relación.
Ejemplo 2: Ingresos y gastos
Imaginemos que queremos estudiar la relación entre los ingresos y los gastos de un grupo de individuos. Calculamos la covarianza y obtenemos un valor negativo. Esto sugiere que a medida que los ingresos de una persona aumentan, sus gastos tienden a disminuir. Esto podría indicar que las personas con mayores ingresos tienden a ahorrar más o gastar menos en proporción a sus ingresos.
Conclusión
La covarianza es una medida estadística que nos permite entender cómo varían dos variables aleatorias en conjunto con respecto a sus medias. Nos proporciona información sobre la relación entre las variables y puede ser positiva, negativa o cero. Es importante tener en cuenta que la covarianza no es comparable entre diferentes pares de variables, ya que depende de las unidades de medida de las variables.