Exploraremos el concepto de vector unitario. Veremos qué es un vector unitario, cómo se define y cómo se utiliza en diferentes contextos. También analizaremos ejemplos para comprender mejor su aplicación en problemas prácticos.
Definición de Vector Unitario
Un vector unitario es un vector que tiene dirección y sentido, pero no tiene dimensión. Su magnitud o módulo es igual a uno. Es adimensional, lo que significa que no tiene una dimensión establecida por sí mismo, sino que toma las dimensiones del vector de referencia del cual se deriva.
Normalización de un Vector
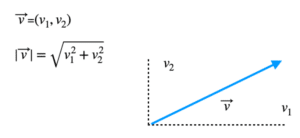
La normalización es el proceso de encontrar un vector con la misma dirección y sentido que el vector original, pero con módulo igual a uno. Para normalizar un vector, se divide cada componente del vector por su magnitud.
Por ejemplo, si tenemos un vector v = (3, 4), su magnitud es √(3^2 + 4^2) = √(9 + 16) = √25 = 5. Para normalizar este vector, dividimos cada componente por su magnitud:
v = (3/5, 4/5)
El vector resultante es un vector unitario en la misma dirección y sentido que el vector original, pero con magnitud igual a uno.
Representación de un Vector Unitario
El vector unitario se representa con una letra y un acento circunflejo o con la letra griega mu y un subíndice. Por ejemplo, un vector unitario en la dirección x se puede representar como «î» o «μx«.
Aplicaciones de los Vectores Unitarios
Los vectores unitarios son ampliamente utilizados en diferentes áreas de la física y las matemáticas. Algunas de las aplicaciones más comunes incluyen:
1. Descomposición de Vectores
Los vectores unitarios se utilizan para descomponer un vector en sus componentes direccionales. Esto es útil para analizar el movimiento de un objeto en diferentes direcciones.
Por ejemplo, si tenemos un vector v = (3, 4), podemos descomponerlo en sus componentes direccionales utilizando los vectores unitarios en las direcciones x e y:
v = 3(î) + 4(ĵ)
Esta descomposición nos permite analizar el movimiento del objeto en la dirección x y en la dirección y por separado.
2. Cálculo de Fuerzas
En física, los vectores unitarios se utilizan para calcular las fuerzas resultantes en un sistema. Al descomponer las fuerzas en sus componentes direccionales, se pueden sumar o restar para obtener la fuerza resultante.
Por ejemplo, si tenemos dos fuerzas F1 = 5(î) y F2 = 3(ĵ), podemos sumar estas fuerzas utilizando los vectores unitarios:
Fresultante = F1 + F2 = 5(î) + 3(ĵ)
La fuerza resultante se obtiene sumando las componentes direccionales de las fuerzas individuales.
3. Coordenadas Polares
En matemáticas, los vectores unitarios se utilizan para representar las coordenadas polares. Los vectores unitarios en las direcciones radial y angular se utilizan para describir la posición y el movimiento de un punto en un sistema de coordenadas polares.
Por ejemplo, en coordenadas polares, un punto se puede representar como (r, θ), donde r es la distancia desde el origen y θ es el ángulo con respecto al eje x. Los vectores unitarios en las direcciones radial y angular se representan como «ŕ̂» y «θ̂», respectivamente.
Ejemplos de Vectores Unitarios
A continuación, se presentan algunos ejemplos de vectores unitarios:
1. Vector Unitario en la Dirección x
El vector unitario en la dirección x se representa como «î» y tiene una magnitud de uno en la dirección x.
2. Vector Unitario en la Dirección y
El vector unitario en la dirección y se representa como «ĵ» y tiene una magnitud de uno en la dirección y.
3. Vector Unitario en la Dirección z
El vector unitario en la dirección z se representa como «k̂» y tiene una magnitud de uno en la dirección z.
4. Vector Unitario en Coordenadas Polares
En coordenadas polares, los vectores unitarios se representan como «ŕ̂» en la dirección radial y «θ̂» en la dirección angular.
Conclusión
Un vector unitario es un vector adimensional con magnitud igual a uno. Se utiliza en diferentes áreas de la física y las matemáticas para representar direcciones y descomponer vectores en sus componentes direccionales. La normalización es el proceso de encontrar un vector unitario a partir de un vector dado. Los vectores unitarios son herramientas fundamentales en el estudio de la física y las matemáticas, y su comprensión es esencial para resolver problemas relacionados con el movimiento, las fuerzas y las coordenadas polares.