Exploraremos el concepto de teorema, su definición y significado, así como algunos ejemplos conocidos. Los teoremas son proposiciones fundamentales en matemáticas que se pueden demostrar de manera lógica a partir de axiomas o de otros teoremas previamente demostrados. Son afirmaciones de gran importancia y tienen aplicaciones tanto en matemáticas como en la vida cotidiana.
Los teoremas son una parte esencial de la matemática y juegan un papel crucial en el desarrollo de la disciplina. A través de la demostración de teoremas, los matemáticos pueden establecer verdades matemáticas y descubrir nuevas relaciones entre diferentes objetos matemáticos. Además, los teoremas también tienen aplicaciones prácticas en la resolución de problemas en diversos campos.
2. Definición de un Teorema
Un teorema es una proposición que puede ser demostrada de manera lógica a partir de axiomas o de otros teoremas previamente demostrados. Antes de ser demostrado, se considera una hipótesis o conjetura. Los teoremas son fundamentales en matemáticas y juegan un papel crucial en el desarrollo de la disciplina.
La demostración de un teorema implica seguir una serie de pasos lógicos y razonamientos para llegar a una conclusión válida. Estos pasos pueden incluir el uso de definiciones, axiomas, leyes y propiedades matemáticas establecidas. Una vez que un teorema ha sido demostrado, se considera una verdad matemática establecida.
3. Significado de un Teorema
Los teoremas son afirmaciones de gran importancia en matemáticas. Una vez que un teorema ha sido demostrado, se considera una verdad matemática establecida. Los teoremas permiten establecer relaciones y propiedades entre diferentes objetos matemáticos, lo que ayuda a comprender y resolver problemas más complejos.
Los teoremas también tienen un significado más amplio en el contexto de la matemática. Representan el resultado de un proceso de razonamiento lógico y riguroso, y demuestran la validez de una afirmación matemática. Los teoremas son la base del conocimiento matemático y proporcionan una estructura sólida para el desarrollo de la disciplina.
4. Ejemplos de Teoremas
4.1 Teorema de Tales
El Teorema de Tales establece que al trazar una línea paralela a uno de los lados de un triángulo, se generan dos triángulos semejantes. Este teorema es ampliamente utilizado en geometría y tiene aplicaciones en la resolución de problemas relacionados con la proporcionalidad de segmentos en triángulos.
El Teorema de Tales se puede enunciar de la siguiente manera: «Si se traza una línea paralela a uno de los lados de un triángulo, los segmentos que se forman en los otros dos lados son proporcionales». Este teorema es útil para resolver problemas de geometría que involucran la proporcionalidad de segmentos en triángulos.
4.2 Teorema de Pitágoras
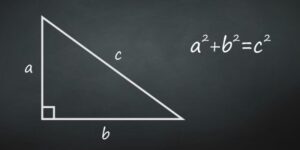
El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Este teorema es uno de los más conocidos y utilizados en matemáticas y tiene aplicaciones en la resolución de problemas relacionados con la longitud de los lados de un triángulo rectángulo.
El Teorema de Pitágoras se puede enunciar de la siguiente manera: «En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos». Este teorema es utilizado para calcular la longitud de los lados de un triángulo rectángulo cuando se conocen las longitudes de los otros dos lados.
5. Aplicaciones de los Teoremas
Los teoremas tienen aplicaciones en diversos campos de la matemática, así como en la vida cotidiana. En matemáticas, los teoremas son utilizados para demostrar resultados y establecer relaciones entre diferentes objetos matemáticos. Los teoremas también son utilizados como herramientas para resolver problemas más complejos y desarrollar nuevas teorías.
En la vida cotidiana, los teoremas pueden ser utilizados para resolver problemas prácticos. Por ejemplo, el Teorema de Pitágoras se puede utilizar para calcular la distancia entre dos puntos en un plano cartesiano. Otro ejemplo es el Teorema de Tales, que se puede utilizar para determinar la altura de un objeto inaccesible midiendo las sombras que proyecta.
6. Conclusiones
Los teoremas son proposiciones fundamentales en matemáticas que se pueden demostrar de manera lógica a partir de axiomas o de otros teoremas previamente demostrados. Son afirmaciones de gran importancia y tienen aplicaciones tanto en matemáticas como en la vida cotidiana. Algunos ejemplos conocidos de teoremas son el Teorema de Tales y el Teorema de Pitágoras.
Los teoremas son esenciales en el desarrollo de la matemática y permiten establecer verdades matemáticas y descubrir nuevas relaciones entre diferentes objetos matemáticos. Además, los teoremas también tienen aplicaciones prácticas en la resolución de problemas en diversos campos. En definitiva, los teoremas son una parte fundamental del conocimiento matemático y juegan un papel crucial en el avance de la disciplina.