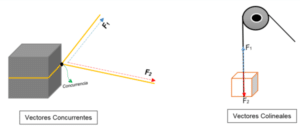
En el ámbito de la geometría y el álgebra lineal, los vectores colineales son aquellos que se encuentran en la misma recta o son paralelos a una cierta recta. Exploraremos en detalle las condiciones que deben cumplir los vectores para ser considerados colineales, así como ejemplos que ilustran estos conceptos.
Condiciones de Colinearidad de Vectores
1. Igualdad de Relaciones entre Coordenadas
Una de las condiciones para que dos vectores sean colineales es que las relaciones entre sus coordenadas sean iguales. Esto significa que si tenemos dos vectores en un plano xy, por ejemplo, (a, b) y (c, d), se debe cumplir la siguiente igualdad: a/c = b/d.
Por ejemplo, consideremos los vectores (2, 4) y (4, 8). Para determinar si son colineales, verifiquemos las condiciones mencionadas anteriormente:
- Relaciones entre coordenadas: 2/4 = 4/8, lo cual es cierto.
Por lo tanto, los vectores (2, 4) y (4, 8) cumplen la condición de igualdad de relaciones entre coordenadas y son colineales.
2. Producto Vectorial Igual a Cero
Otra condición para la colinearidad de vectores es que el producto vectorial entre ellos sea igual a cero. El producto vectorial se calcula multiplicando las coordenadas correspondientes de los vectores y restando los productos resultantes. Si el resultado es cero, los vectores son colineales.
Por ejemplo, consideremos los vectores (1, 2, 3) y (2, 4, 6). Veamos si cumplen las condiciones de colinearidad:
- Producto vectorial: (1 * 4 – 2 * 2) – (1 * 6 – 2 * 3) + (2 * 6 – 4 * 3) = 0 – 3 + 0 = -3, lo cual no es igual a cero.
Por lo tanto, los vectores (1, 2, 3) y (2, 4, 6) no cumplen la condición de producto vectorial igual a cero y no son colineales.
Ejemplos de Vectores Colineales
Ejemplo 1: Vectores en el Plano xy
Consideremos dos vectores en el plano xy: (2, 4) y (4, 8). Para determinar si son colineales, verifiquemos las condiciones mencionadas anteriormente:
- Relaciones entre coordenadas: 2/4 = 4/8, lo cual es cierto.
- Producto vectorial: (2 * 8) – (4 * 4) = 16 – 16 = 0, lo cual también es cierto.
Por lo tanto, los vectores (2, 4) y (4, 8) son colineales.
Ejemplo 2: Vectores en el Espacio tridimensional
Supongamos que tenemos dos vectores en el espacio tridimensional: (1, 2, 3) y (2, 4, 6). Veamos si cumplen las condiciones de colinearidad:
- Relaciones entre coordenadas: 1/2 = 2/4 = 3/6, lo cual es cierto.
- Producto vectorial: (1 * 4 – 2 * 2) – (1 * 6 – 2 * 3) + (2 * 6 – 4 * 3) = 0 – 3 + 0 = -3, lo cual no es igual a cero.
Por lo tanto, los vectores (1, 2, 3) y (2, 4, 6) no son colineales.
Conclusiones
Los vectores son colineales cuando tienen la misma dirección y cumplen las condiciones de igualdad entre sus coordenadas y producto vectorial igual a cero. Estas condiciones nos permiten determinar si dos vectores son colineales o no, lo cual es útil en diversos contextos geométricos y algebraicos.