El triángulo es una figura geométrica básica y fundamental en la geometría. Está conformado por tres lados, tres vértices y tres ángulos interiores. Exploraremos en detalle la definición del triángulo, sus elementos principales y algunos ejemplos comunes.
Definición de Triángulo
Un triángulo es un polígono de tres lados, tres vértices y tres ángulos interiores. Es una figura plana que se encuentra en el plano euclidiano y es considerada una de las formas más simples de polígonos. Los triángulos pueden tener diferentes formas y tamaños, pero siempre conservan la característica de tener tres lados.
Elementos de un Triángulo
Los elementos principales de un triángulo son:
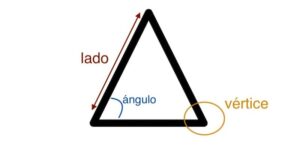
- Vértices: Son los puntos donde se encuentran los lados del triángulo. Un triángulo tiene tres vértices.
- Lados: Son las líneas que conectan los vértices del triángulo. Un triángulo tiene tres lados.
- Ángulos interiores: Son los ángulos formados por los lados del triángulo en su interior. Un triángulo tiene tres ángulos interiores.
Los vértices del triángulo se representan con letras mayúsculas, como A, B y C. Los lados se representan con letras minúsculas, como a, b y c. Los ángulos se representan con letras griegas, como α, β y γ.
Tipos de Triángulos
Existen diferentes tipos de triángulos, clasificados según las características de sus lados y ángulos:
- Triángulo Equilátero: Tiene los tres lados y los tres ángulos interiores iguales. Es decir, todos sus lados miden lo mismo y todos sus ángulos miden 60 grados.
- Triángulo Isósceles: Tiene dos lados iguales y dos ángulos interiores iguales. El tercer lado y el tercer ángulo son diferentes.
- Triángulo Escaleno: Tiene los tres lados y los tres ángulos interiores diferentes. Ninguno de sus lados ni ángulos son iguales.
- Triángulo Rectángulo: Tiene un ángulo interior de 90 grados, llamado ángulo recto. Los otros dos ángulos interiores suman 90 grados.
Estos son solo algunos ejemplos de los tipos de triángulos que existen. También se pueden encontrar triángulos con combinaciones de estas características, como un triángulo isósceles y rectángulo.
Triángulos en Otras Figuras Geométricas
Además de encontrarse como una figura independiente, los triángulos también pueden encontrarse en otras figuras geométricas. Por ejemplo:
- Cuadrado: Cuando se trazan las diagonales de un cuadrado, se forman cuatro triángulos congruentes.
- Rectángulo: Al igual que el cuadrado, al trazar las diagonales de un rectángulo se forman dos triángulos congruentes.
- Pentágono: Al trazar diagonales desde un vértice de un pentágono regular, se forman cinco triángulos congruentes.
Estos son solo algunos ejemplos de cómo los triángulos pueden estar presentes en otras figuras geométricas.
Propiedades de los Triángulos
Además de sus elementos principales y tipos, los triángulos tienen algunas propiedades importantes:
- Ángulos Interiores: La suma de los ángulos interiores de un triángulo siempre es igual a 180 grados. Es decir, α + β + γ = 180°.
- Ángulos Exteriores: Los ángulos exteriores de un triángulo son suplementarios a los ángulos interiores del mismo lado. Es decir, α’ + β’ + γ’ = 360°.
- Perímetro: El perímetro de un triángulo se calcula sumando la longitud de sus tres lados. Es decir, perímetro = a + b + c.
- Área: El área de un triángulo se puede encontrar multiplicando la longitud de una base por su altura y dividiendo entre dos. Es decir, área = (base * altura) / 2.
Triángulo Rectángulo
En el caso de un triángulo rectángulo, la base y la altura son los lados que forman el ángulo recto. El lado opuesto al ángulo recto se llama hipotenusa. El teorema de Pitágoras se aplica a los triángulos rectángulos y establece que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados. Es decir, a^2 + b^2 = c^2.
Conclusiones
El triángulo es una figura geométrica básica y fundamental en la geometría. Tiene tres lados, tres vértices y tres ángulos interiores. Existen diferentes tipos de triángulos, como el equilátero, isósceles, escaleno y rectángulo. Los triángulos también pueden encontrarse en otras figuras geométricas. Además, los triángulos tienen propiedades importantes, como la suma de los ángulos interiores, los ángulos exteriores, el perímetro y el área.