El triángulo equilátero es una figura geométrica que ha despertado la curiosidad del ser humano desde la antigüedad, debido a su simetría y perfección. Pero ¿qué sabemos realmente sobre esta forma tan interesante? En este artículo, te invitamos a descubrir la definición y características de este polígono, considerado uno de los más importantes en el mundo de las matemáticas y la geometría. Acompáñanos en este recorrido por su historia, propiedades y aplicaciones, y conoce los fascinantes secretos que esconde detrás de sus tres lados iguales. ¡Prepárate para explorar el mundo del triángulo equilátero de una manera única y emocionante!
Definición
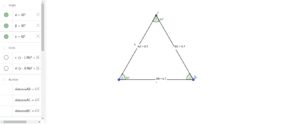
El triángulo equilátero es un tipo de triángulo que se caracteriza por tener sus tres lados de igual longitud y sus tres ángulos internos de igual medida.
Características
Lados de igual longitud
Un triángulo equilátero tiene la particularidad de que sus tres lados miden la misma longitud. Esto significa que los segmentos que unen los vértices del triángulo son iguales entre sí.
Ángulos internos iguales
Los tres ángulos internos de un triángulo equilátero tienen la misma medida, que es de 60 grados. Esto se debe a que la suma de los ángulos internos de cualquier triángulo siempre es igual a 180 grados.
Polígono regular
El triángulo equilátero es un polígono regular, lo que significa que todos sus lados y ángulos son iguales. Esta regularidad le confiere una simetría especial y lo distingue de otros tipos de triángulos.
Triángulo acutángulo
El triángulo equilátero es también un triángulo acutángulo, lo que significa que todos sus ángulos internos son menores a 90 grados. En el caso del triángulo equilátero, todos sus ángulos miden exactamente 60 grados.
Perímetro
El perímetro de un triángulo equilátero se calcula sumando la longitud de sus tres lados. Dado que todos los lados son iguales, el perímetro se obtiene multiplicando la longitud de uno de los lados por 3.
Área
El área de un triángulo equilátero se puede calcular utilizando la fórmula de Herón, que es una fórmula general para calcular el área de cualquier triángulo. La fórmula de Herón utiliza la longitud de los lados del triángulo para determinar su área.