Aceleración Tangencial

La aceleración tangencial es una medida de los cambios en la velocidad de un objeto en movimiento a lo largo de una trayectoria curva. En este artículo, exploraremos en detalle la fórmula para calcular la aceleración tangencial, su definición y algunos ejemplos para comprender mejor su aplicación en la física.

Definición de la aceleración tangencial

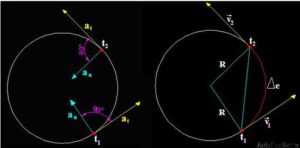
La aceleración tangencial es una magnitud vectorial que indica cómo cambia la velocidad de un objeto en movimiento a lo largo de una trayectoria curva. Se representa por el vector a_t y se calcula utilizando la siguiente fórmula:

a_t = dv/dt * u_t

Donde:

• a_t es el vector aceleración tangencial
• dv/dt es la derivada del vector velocidad con respecto al tiempo
• u_t es el vector unitario con la dirección del eje tangente y sentido del movimiento

Cálculo de la aceleración tangencial

Para calcular la aceleración tangencial, se deben seguir los siguientes pasos:

Lee TambiénAceleración Centrífuga

1. Calcular la derivada del vector velocidad con respecto al tiempo (dv/dt)
2. Obtener el módulo de la velocidad (v)
3. Calcular el vector unitario con la dirección del eje tangente y sentido del movimiento (u_t)
4. Multiplicar dv/dt por v y u_t para obtener el vector aceleración tangencial (a_t)

Ejemplos de aceleración tangencial

Ejemplo 1: Movimiento acelerado

Supongamos que un automóvil está acelerando en una curva. La velocidad del automóvil aumenta de 20 m/s a 30 m/s en un intervalo de tiempo de 5 segundos. Para calcular la aceleración tangencial, seguimos los pasos mencionados anteriormente:

1. Calculamos la derivada del vector velocidad con respecto al tiempo: dv/dt = (30 m/s - 20 m/s) / 5 s = 2 m/s²
2. Obtenemos el módulo de la velocidad: v = 30 m/s
3. Calculamos el vector unitario con la dirección del eje tangente y sentido del movimiento: u_t = dirección del movimiento
4. Multiplicamos dv/dt por v y u_t para obtener el vector aceleración tangencial: a_t = 2 m/s² * 30 m/s * u_t

En este caso, la aceleración tangencial tiene un valor mayor que cero (> 0) debido a que el automóvil está acelerando en la curva.

Ejemplo 2: Movimiento retardado

Imaginemos ahora que un objeto se desliza por un tobogán y su velocidad disminuye de 10 m/s a 5 m/s en un intervalo de tiempo de 2 segundos. Para calcular la aceleración tangencial, seguimos los mismos pasos mencionados anteriormente:

1. Calculamos la derivada del vector velocidad con respecto al tiempo: dv/dt = (5 m/s - 10 m/s) / 2 s = -2.5 m/s²
2. Obtenemos el módulo de la velocidad: v = 5 m/s
3. Calculamos el vector unitario con la dirección del eje tangente y sentido del movimiento: u_t = dirección del movimiento
4. Multiplicamos dv/dt por v y u_t para obtener el vector aceleración tangencial: a_t = -2.5 m/s² * 5 m/s * u_t

En este caso, la aceleración tangencial tiene un valor menor que cero (< 0) debido a que el objeto está desacelerando en el tobogán.

Ejemplo 3: Movimiento uniforme

Supongamos que un objeto se mueve en una trayectoria circular a una velocidad constante de 15 m/s. En este caso, la velocidad no cambia en el tiempo, por lo que la derivada del vector velocidad con respecto al tiempo es cero (dv/dt = 0). Por lo tanto, la aceleración tangencial también es cero (a_t = 0 m/s²). En un movimiento uniforme, la aceleración tangencial es igual a cero (= 0).

Lee TambiénAcoplamiento

Conclusiones

La aceleración tangencial es una medida de los cambios en la velocidad de un objeto en movimiento a lo largo de una trayectoria curva. Se calcula utilizando la fórmula a_t = dv/dt * u_t, donde dv/dt es la derivada del vector velocidad con respecto al tiempo y u_t es el vector unitario con la dirección del eje tangente y sentido del movimiento. La aceleración tangencial puede ser mayor que cero (> 0) en un movimiento acelerado, menor que cero (< 0) en un movimiento retardado o decelerado, o igual a cero (= 0) en un movimiento uniforme.