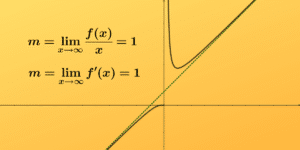Exploraremos en detalle el concepto de asíntota. Veremos qué es una asíntota, cómo se clasifican y cómo se utilizan en la representación gráfica de curvas y funciones. También analizaremos ejemplos para comprender mejor este concepto matemático.
Una asíntota es una recta que se acerca indefinidamente a una curva o función, pero sin llegar a intersectarla. Puede ser horizontal, vertical u oblicua, dependiendo de su posición relativa a los ejes. Las asíntotas son útiles para representar gráficamente una curva y se utilizan en campos como la ingeniería y la arquitectura. El término asíntota proviene del griego y significa «que no cae junto». Fue utilizado por primera vez por el geómetra Apolonio de Perge en su tratado sobre las secciones cónicas.
Definición de Asíntota
Una asíntota es una recta que se acerca indefinidamente a una curva o función, pero sin llegar a intersectarla. Es decir, a medida que nos alejamos de la curva, la recta se acerca cada vez más a ella, pero nunca la toca.
Las asíntotas pueden ser horizontales, verticales u oblicuas, dependiendo de su posición relativa a los ejes. Las asíntotas horizontales son rectas paralelas al eje x que se acercan a la curva a medida que nos alejamos hacia los extremos del eje x. Las asíntotas verticales son rectas paralelas al eje y que se acercan a la curva a medida que nos alejamos hacia los extremos del eje y. Las asíntotas oblicuas son rectas que no son ni horizontales ni verticales y se acercan a la curva a medida que nos alejamos hacia los extremos del eje x.
Tipos de Asíntotas
Existen tres tipos principales de asíntotas: horizontal, vertical y oblicua. La clasificación de la asíntota depende de su posición relativa a los ejes.
Asíntota Horizontal
Una asíntota horizontal es una recta paralela al eje x que se acerca a la curva a medida que nos alejamos hacia los extremos del eje x. Para determinar si una función tiene una asíntota horizontal, se deben analizar los límites de la función cuando x tiende a infinito o menos infinito.
Por ejemplo, consideremos la función f(x) = 1/x. A medida que x tiende a infinito o menos infinito, la función se acerca cada vez más a cero, pero nunca la alcanza. Por lo tanto, la recta y = 0 es una asíntota horizontal de la función.
Asíntota Vertical
Una asíntota vertical es una recta paralela al eje y que se acerca a la curva a medida que nos alejamos hacia los extremos del eje y. Para determinar si una función tiene una asíntota vertical, se deben analizar los límites de la función cuando x tiende a un valor constante.
Por ejemplo, consideremos la función f(x) = 1/(x-2). A medida que x se acerca a 2, la función tiende a infinito o menos infinito, pero nunca alcanza un valor constante. Por lo tanto, la recta x = 2 es una asíntota vertical de la función.
Asíntota Oblicua
Una asíntota oblicua es una recta que no es ni horizontal ni vertical y se acerca a la curva a medida que nos alejamos hacia los extremos del eje x. Para determinar si una función tiene una asíntota oblicua, se deben analizar los límites de la función cuando x tiende a infinito o menos infinito.
Por ejemplo, consideremos la función f(x) = x + 1. A medida que x tiende a infinito o menos infinito, la función se acerca cada vez más a la recta y = x. Por lo tanto, la recta y = x es una asíntota oblicua de la función.
Utilidad de las Asíntotas
Las asíntotas son herramientas útiles en la representación gráfica de curvas y funciones. Nos permiten tener una idea clara de cómo se comporta una función en los extremos y nos ayudan a trazar la curva de manera más precisa. Las asíntotas también se utilizan en campos como la ingeniería y la arquitectura para diseñar estructuras y sistemas.
Por ejemplo, en la ingeniería civil, las asíntotas se utilizan para diseñar puentes y estructuras que deben soportar cargas extremas. Al comprender las asíntotas de una función que representa la carga sobre una estructura, los ingenieros pueden diseñar de manera más eficiente los materiales y la geometría de la estructura para garantizar su estabilidad.
Ejemplos de Asíntotas
A continuación, se presentan algunos ejemplos de asíntotas:
Ejemplo 1: Asíntota Horizontal
La función f(x) = 1/x tiene una asíntota horizontal en y = 0. A medida que x tiende a infinito o menos infinito, la función se acerca cada vez más a cero, pero nunca la alcanza.
Ejemplo 2: Asíntota Vertical
La función f(x) = 1/(x-2) tiene una asíntota vertical en x = 2. A medida que x se acerca a 2, la función tiende a infinito o menos infinito, pero nunca alcanza un valor constante.
Ejemplo 3: Asíntota Oblicua
La función f(x) = x + 1 tiene una asíntota oblicua en y = x. A medida que x tiende a infinito o menos infinito, la función se acerca cada vez más a la recta y = x.
Conclusión
Las asíntotas son rectas que se acercan indefinidamente a una curva o función sin llegar a intersectarla. Pueden ser horizontales, verticales u oblicuas, dependiendo de su posición relativa a los ejes. Las asíntotas son útiles en la representación gráfica de curvas y funciones, y se utilizan en diversos campos como la ingeniería y la arquitectura. Comprender el concepto de asíntota nos permite tener una mejor comprensión de las propiedades y comportamiento de las funciones.