Cero
El cero es un número fundamental en las matemáticas y en diferentes contextos. Exploraremos la definición y el concepto del cero, así como su importancia en diversas áreas.
El cero es el número que representa la ausencia de cantidad o valor nulo. En matemáticas, se utiliza como punto de partida, de origen y como divisor entre números positivos y negativos. También se utiliza en sistemas de numeración, como el decimal, binario y hexadecimal, donde su función puede variar.
Origen etimológico
La palabra "cero" tiene su origen en el árabe clásico y se ha transmitido a través de diferentes lenguajes. En árabe, se utilizaba la palabra "sifr" para referirse al cero, que significa "vacío" o "nada". Esta palabra se introdujo en Europa a través de la cultura árabe y se adoptó en diferentes idiomas.
Importancia del cero en las matemáticas
El cero es fundamental en las operaciones matemáticas y en la determinación de reglas para el resto de los números. Algunos aspectos importantes del cero en las matemáticas son:
Punto de partida y origen
El cero se utiliza como punto de partida en muchas operaciones matemáticas. Por ejemplo, en la recta numérica, el cero es el punto de origen desde el cual se representan los números positivos y negativos.
CentímetroEn las operaciones de suma y resta, el cero actúa como el elemento neutro. Al sumar cero a cualquier número, el resultado es el mismo número. Al restar cero de cualquier número, el resultado también es el mismo número.
Divisor entre números positivos y negativos
El cero actúa como divisor entre números positivos y negativos. Los números a la derecha del cero son positivos, mientras que los números a la izquierda del cero son negativos.
Por ejemplo, si tenemos los números -3, -2, -1, 0, 1, 2, 3, el cero divide claramente los números negativos de los positivos.
Sistemas de numeración
El cero se utiliza en diferentes sistemas de numeración, como el decimal, binario y hexadecimal. En el sistema decimal, el cero se utiliza para representar la ausencia de unidades en una posición determinada.
En el sistema binario, el cero representa la ausencia de una cantidad y el uno representa la presencia de esa cantidad. Por ejemplo, en el número binario 1010, el cero en la segunda posición indica que no hay dos unidades presentes.
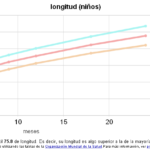PercentilEn el sistema hexadecimal, el cero se utiliza para representar la ausencia de una cantidad en una posición determinada. Por ejemplo, en el número hexadecimal 1A3, el cero en la segunda posición indica que no hay dieciséis unidades presentes.
El cero en diferentes contextos
Además de su importancia en las matemáticas, el cero puede referirse a la falta absoluta o completa de algo en diferentes contextos. Algunos ejemplos son:
Cero absoluto en temperatura
En la escala Kelvin, el cero absoluto es la temperatura más baja posible, donde las partículas no tienen movimiento térmico. Se representa como 0 K.
El cero absoluto es utilizado como referencia para medir otras temperaturas. Por ejemplo, en la escala Celsius, el cero absoluto corresponde a -273.15 grados Celsius.
Cero en mediciones
En algunas mediciones, el cero se utiliza como referencia para indicar la ausencia de una cantidad. Por ejemplo, en una balanza, el cero se establece como el punto de equilibrio donde no hay peso.
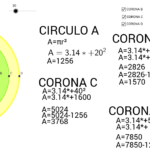Corona CircularEn la medición de tiempo, el cero se utiliza como referencia para indicar el inicio de un evento o el punto de partida de un intervalo de tiempo.
Cero en estadísticas
En estadísticas, el cero puede representar la falta de ocurrencia de un evento o la ausencia de una característica en un conjunto de datos.
Por ejemplo, si se realiza un estudio sobre la cantidad de accidentes de tráfico en una ciudad durante un año, si no se registra ningún accidente en un mes determinado, se puede decir que hubo cero accidentes en ese mes.
Conclusiones
El cero es un número fundamental en las matemáticas y en diferentes contextos. Representa la ausencia de cantidad o valor nulo y se utiliza como punto de partida, divisor y referencia en diversas operaciones y sistemas de numeración. Además, el cero puede referirse a la falta absoluta o completa de algo en diferentes contextos.
También te puede interesar: