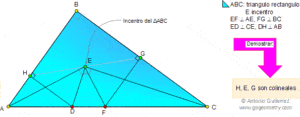
En el campo de la geometría, el término «colineales» se utiliza para describir puntos que se encuentran en la misma recta. Exploraremos en detalle la definición de colineales, su importancia en la geometría y proporcionaremos ejemplos para una mejor comprensión.
Definición de colineales
El adjetivo colineal se emplea en el terreno de la geometría para calificar al punto que está ubicado en la misma recta que otro punto.
Concepto de punto en geometría
Los puntos son figuras geométricas que, sin volumen, área, longitud ni dimensión, permiten describir una cierta posición en el espacio, a partir de un sistema de coordenadas ya establecido.
Concepto de recta en geometría
Una recta es una sucesión infinita de puntos que se desarrolla en una misma dirección. Gráficamente, una recta es una línea que podría extenderse indefinidamente tanto hacia atrás como hacia delante, siempre en la misma dirección.
Ejemplos de puntos colineales
Para comprender mejor el concepto de colineales, veamos algunos ejemplos:
Ejemplo 1
En la recta A, se encuentran los puntos r, s y t. Estos tres puntos son colineales ya que se encuentran en la misma recta.
Ejemplo 2
En la recta B, se encuentran los puntos k y l. Estos dos puntos también son colineales ya que se encuentran en la misma recta.
Ejemplo 3
En cambio, si en la recta A se encuentra el punto r y en la recta B se halla el punto k, estos dos puntos (r y k) no son colineales debido a que pertenecen a rectas distintas.
Importancia de las rectas y puntos en geometría
Es importante destacar que las rectas y los puntos son conceptos abstractos en geometría. No son objetos físicos que se puedan trazar en una hoja de papel o en una pared, sino que son elementos teóricos utilizados para describir posiciones en el espacio.
Colinealidad de segmentos
Los segmentos también pueden ser colineales. Un segmento es una porción de recta que se desarrolla entre dos puntos extremos. Cuando dos segmentos comparten un punto extremo, se denominan segmentos consecutivos y son colineales si se encuentran en la misma recta. Por otro lado, si los segmentos consecutivos se desarrollan en rectas diferentes, se consideran segmentos no colineales.
Operaciones con segmentos colineales
En cuanto a las operaciones que se pueden realizar con segmentos colineales, si se suman dos o más segmentos consecutivos colineales, se obtiene un nuevo segmento que está determinado por los extremos no comunes del conjunto. Desde un punto de vista geométrico, esta operación resulta en un nuevo segmento que se puede construir ordenando los segmentos originales de forma colineal hasta encontrar uno cuyos extremos sean uno de cada punto del primero y el último.
Conclusiones
Los puntos colineales son aquellos que se encuentran en la misma recta. Este concepto es fundamental en la geometría y se utiliza para describir la posición de puntos y segmentos en el espacio. Comprender la colinealidad es esencial para el estudio y la aplicación de la geometría en diversos campos.