Exploraremos en detalle la cotangente, una función trigonométrica fundamental en matemáticas. Veremos su definición, concepto, propiedades y aplicaciones en diferentes áreas.
Definición de la cotangente
La cotangente es una función trigonométrica que se define como el cociente entre el cateto adyacente y el cateto opuesto de un triángulo rectángulo. Es la función inversa de la tangente y se representa como cot(x) o ctn(x), donde x es el ángulo.
Concepto de la cotangente
La cotangente se utiliza para calcular la relación entre los lados de un triángulo rectángulo y se puede expresar de dos formas: como el cociente entre el cateto adyacente y el cateto opuesto, o como el cociente entre 1 y la tangente del ángulo.
Propiedades de la cotangente
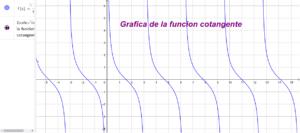
- La cotangente es una función periódica con un período de π.
- Su dominio es el conjunto de todos los ángulos excepto aquellos en los que la tangente es cero, es decir, los ángulos de 90 grados más múltiplos enteros de π.
- Su recorrido es el conjunto de todos los números reales.
- La cotangente es una función decreciente en su dominio.
- No está definida para ángulos de 90 grados más múltiplos enteros de π.
- Se puede expresar en términos de la seno y el coseno como el cociente entre el coseno y el seno del ángulo.
- Es el inverso multiplicativo de la tangente, lo que significa que el producto de la tangente y la cotangente de un ángulo es siempre igual a 1.
Aplicaciones de la cotangente
La cotangente se utiliza en una variedad de aplicaciones en matemáticas y física. Algunos ejemplos incluyen:
Trigonometría
Se utiliza en el cálculo de ángulos y distancias en trigonometría.
Ingeniería
Se utiliza en el análisis de circuitos eléctricos en ingeniería.
Física
Se utiliza en la resolución de problemas de movimiento y fuerza en física.
Conclusión
La cotangente es una función trigonométrica que se define como el cociente entre el cateto adyacente y el cateto opuesto de un triángulo rectángulo. Es la función inversa de la tangente y se utiliza para calcular la relación entre los lados de un triángulo rectángulo. Tiene propiedades importantes como su periodicidad, dominio y recorrido, y se utiliza en una variedad de aplicaciones en matemáticas y física.