División

La división es una operación matemática fundamental que nos permite descomponer un número en partes iguales según otro número. Es una de las cuatro operaciones básicas de la aritmética y es la operación opuesta a la multiplicación. Exploraremos en detalle la definición, el concepto y algunos ejemplos de la división.

La división es una operación matemática que consiste en descomponer un número, llamado dividendo, en partes iguales según otro número, llamado divisor. El resultado de la división se llama cociente. El símbolo utilizado para representar la división es el óbelo (÷), aunque también se pueden utilizar dos puntos (:), una barra inclinada (/) o una barra horizontal (–).

Términos de la División

En una operación de división, se utilizan varios términos clave:

• Dividendo: Es el número que se va a dividir.
• Divisor: Es el número por el cual se divide el dividendo.
• Cociente: Es el resultado de la división, es decir, el número de partes iguales en las que se divide el dividendo.
• Residuo: Es el número que queda después de realizar la división, cuando el dividendo no se puede dividir exactamente por el divisor.

Concepto de la División

El concepto de la división se basa en la idea de repartir una cantidad en partes iguales. Por ejemplo, si tenemos 12 galletas y queremos repartirlas entre 3 personas, podemos utilizar la división para determinar cuántas galletas le corresponden a cada persona. En este caso, el dividendo sería 12, el divisor sería 3 y el cociente sería 4, lo que significa que cada persona recibiría 4 galletas.

Propiedades de la División

La división tiene varias propiedades importantes:

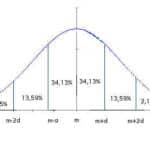Lee TambiénCurva Normal

• Propiedad Conmutativa: El orden de los números en una división no afecta el resultado. Por ejemplo, 12 ÷ 3 es igual a 3 ÷ 12.
• Propiedad Asociativa: El agrupamiento de los números en una división no afecta el resultado. Por ejemplo, (12 ÷ 3) ÷ 2 es igual a 12 ÷ (3 ÷ 2).
• Propiedad Distributiva: La división se distribuye sobre la suma y la resta. Por ejemplo, 12 ÷ (3 + 2) es igual a (12 ÷ 3) + (12 ÷ 2).
• Propiedad de la División por Cero: No se puede dividir entre cero. La división por cero es indefinida.

Ejemplos de División

A continuación, se presentan algunos ejemplos de divisiones:

Ejemplo 1

Dividendo: 15

Divisor: 3

Cociente: 5

Residuo: 0

Lee TambiénCircunferencia

En este caso, 15 dividido por 3 es igual a 5 sin residuo.

Ejemplo 2

Dividendo: 20

Divisor: 7

Cociente: 2

Residuo: 6

Lee TambiénPrueba De Hipótesis

En este caso, 20 dividido por 7 es igual a 2 con un residuo de 6.

Ejemplo 3

Dividendo: 10

Divisor: 4

Cociente: 2.5

En este caso, 10 dividido por 4 es igual a 2.5, lo que significa que no se puede dividir exactamente y el resultado es un número decimal.

Conclusión

La división es una operación matemática esencial que nos permite descomponer un número en partes iguales según otro número. Es importante comprender los términos y propiedades de la división para poder resolver problemas matemáticos y realizar cálculos precisos. Esperamos que este artículo haya sido útil para comprender la definición y el concepto de la división.