Exploraremos en detalle la función cuadrática, su definición, concepto y algunas aplicaciones prácticas. La función cuadrática es una de las funciones más importantes en matemáticas y se utiliza ampliamente en diversos campos. Comenzaremos por comprender su definición y características básicas.
Definición de la función cuadrática
La función cuadrática es un tipo de función polinómica de segundo grado. Se representa mediante la expresión:
f(x) = ax^2 + bx + c
Donde a, b y c son constantes, y a no puede ser igual a cero. Esta restricción es necesaria para que la función cuadrática sea realmente de segundo grado.
Características de la función cuadrática
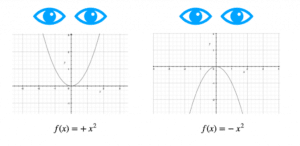
- La gráfica de una función cuadrática es una parábola.
- La parábola puede abrir hacia arriba si a es positivo, o hacia abajo si a es negativo.
- La función cuadrática tiene simetría con respecto al eje vertical.
- La parábola puede tener un máximo o mínimo, dependiendo del signo de a.
Estas características son fundamentales para comprender y analizar la función cuadrática.
Representación de la función cuadrática
Además de la forma de función, la función cuadrática también se puede representar como una ecuación cuadrática de la forma:
ax^2 + bx + c = 0
Esta forma de ecuación cuadrática es útil para resolver problemas y encontrar las raíces de la función cuadrática.
Gráfica de la función cuadrática
La gráfica de una función cuadrática es una parábola. La forma de la parábola y su posición en el plano cartesiano dependen de los valores de a, b y c.
Si a es positivo, la parábola abrirá hacia arriba y tendrá un mínimo en el vértice. Si a es negativo, la parábola abrirá hacia abajo y tendrá un máximo en el vértice.
El vértice de la parábola se encuentra en el punto (-b/2a, f(-b/2a)). Este punto es el punto de simetría de la parábola.
Ejemplos de función cuadrática
Veamos algunos ejemplos de función cuadrática:
Ejemplo 1
Consideremos la función cuadrática f(x) = 2x^2 – 3x + 1.
Para graficar esta función, podemos encontrar el vértice utilizando la fórmula del vértice: x = -b/2a.
En este caso, a = 2 y b = -3. Sustituyendo estos valores en la fórmula, obtenemos x = -(-3)/(2*2) = 3/4.
Para encontrar el valor de f(x) en el vértice, sustituimos x = 3/4 en la función: f(3/4) = 2(3/4)^2 – 3(3/4) + 1 = 2(9/16) – 9/4 + 1 = 9/8 – 9/4 + 1 = 1/8.
Por lo tanto, el vértice de la parábola es (3/4, 1/8).
Podemos graficar la función cuadrática utilizando el vértice y algunos puntos adicionales.
Ejemplo 2
Consideremos la función cuadrática f(x) = -x^2 + 4x – 3.
En este caso, a = -1 y b = 4. Utilizando la fórmula del vértice, encontramos x = -b/2a = -4/(-2) = 2.
Sustituyendo x = 2 en la función, obtenemos f(2) = -(2)^2 + 4(2) – 3 = -4 + 8 – 3 = 1.
Por lo tanto, el vértice de la parábola es (2, 1).
Podemos graficar la función cuadrática utilizando el vértice y algunos puntos adicionales.
Aplicaciones de la función cuadrática
La función cuadrática se utiliza en diversos campos para modelar fenómenos y resolver problemas. Algunas aplicaciones comunes incluyen:
Física
En física, la función cuadrática se utiliza para modelar el movimiento de objetos en caída libre, el lanzamiento de proyectiles y otros fenómenos relacionados con la aceleración y la gravedad.
Economía
En economía, la función cuadrática se utiliza para modelar la oferta y la demanda de productos, la maximización de beneficios y otros problemas relacionados con la optimización.
Ingeniería
En ingeniería, la función cuadrática se utiliza para modelar el comportamiento de estructuras, la optimización de diseños y otros problemas relacionados con la mecánica y la resistencia de materiales.
Conclusión
La función cuadrática es una herramienta poderosa en matemáticas y tiene numerosas aplicaciones en diversos campos. Su forma de parábola y sus propiedades la hacen muy útil para modelar fenómenos y resolver problemas. Esperamos que este artículo te haya ayudado a comprender mejor la función cuadrática y su importancia en el mundo real.