Geometría Analítica
La geometría analítica es una rama de la geometría que combina el álgebra y la geometría para estudiar las figuras geométricas a través de un sistema de coordenadas. Se utiliza el plano cartesiano, que consiste en dos ejes perpendiculares, el eje de abscisas (X) y el eje de ordenadas (Y), para localizar cada punto en el plano. Cada punto se representa por un par ordenado (X, Y).
La geometría analítica permite describir figuras geométricas mediante ecuaciones algebraicas, como rectas, círculos y parábolas. Se considera que René Descartes es el padre de la geometría analítica, ya que fue el primero en proponer la unión del álgebra y la geometría en su obra "La Géométrie".
Historia de la Geometría Analítica
En este apartado se describirá la historia de la geometría analítica, desde sus inicios con René Descartes hasta su desarrollo actual.
René Descartes y "La Géométrie"
René Descartes, filósofo y matemático francés del siglo XVII, es considerado el padre de la geometría analítica. En su obra "La Géométrie", publicada en 1637, Descartes propuso la unión del álgebra y la geometría, sentando las bases de la geometría analítica.
En "La Géométrie", Descartes introdujo el concepto de coordenadas cartesianas, que permiten representar puntos en el plano mediante pares ordenados de números. Estas coordenadas se utilizan para describir la posición de los puntos en relación con los ejes de abscisas y ordenadas.
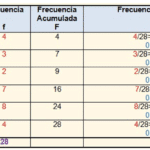Frecuencia RelativaDescartes también desarrolló la idea de que las figuras geométricas pueden ser representadas mediante ecuaciones algebraicas. Por ejemplo, una recta puede ser representada mediante una ecuación lineal, un círculo mediante una ecuación cuadrática, y así sucesivamente.
Desarrollo posterior de la Geometría Analítica
Después de Descartes, otros matemáticos continuaron desarrollando la geometría analítica y aplicándola en diferentes campos.
Pierre de Fermat, matemático francés del siglo XVII, realizó importantes contribuciones a la geometría analítica. Fermat introdujo el concepto de tangente a una curva y desarrolló métodos para encontrar las tangentes a diferentes tipos de curvas.
Blaise Pascal, otro matemático francés del siglo XVII, también hizo importantes avances en la geometría analítica. Pascal desarrolló el concepto de polígonos inscritos y circunscritos, y demostró que los puntos de intersección de las diagonales de un hexágono inscrito forman un hexágono regular.
A lo largo de los siglos, la geometría analítica ha seguido evolucionando y se ha aplicado en diversos campos, como la física, la ingeniería y la computación.
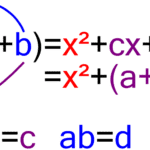FactorizaciónConceptos Fundamentales de la Geometría Analítica
En este apartado se explicarán los conceptos fundamentales de la geometría analítica, como el plano cartesiano, las coordenadas, las ecuaciones de rectas y curvas, entre otros.
Plano Cartesiano
El plano cartesiano es un sistema de coordenadas que se utiliza en la geometría analítica para representar puntos en el espacio. Consiste en dos ejes perpendiculares, el eje de abscisas (X) y el eje de ordenadas (Y).
El eje de abscisas se representa horizontalmente y el eje de ordenadas verticalmente. El punto de intersección de ambos ejes se conoce como origen, y se representa como (0, 0).
Para localizar un punto en el plano cartesiano, se utiliza un par ordenado de números (X, Y), donde X representa la posición del punto en el eje de abscisas y Y representa la posición del punto en el eje de ordenadas.
Coordenadas
Las coordenadas son los valores numéricos que representan la posición de un punto en el plano cartesiano. Se utilizan pares ordenados de números (X, Y) para representar las coordenadas de un punto.
EstadísticaLa coordenada X representa la posición del punto en el eje de abscisas, mientras que la coordenada Y representa la posición del punto en el eje de ordenadas.
Por ejemplo, el punto A con coordenadas (2, 3) se encuentra a dos unidades a la derecha del origen en el eje de abscisas y a tres unidades hacia arriba en el eje de ordenadas.
Ecuaciones de Rectas
Las rectas en el plano cartesiano pueden ser representadas mediante ecuaciones algebraicas. Existen diferentes formas de representar una recta, como la forma general y la forma punto-pendiente.
La forma general de la ecuación de una recta es Ax + By + C = 0, donde A, B y C son constantes y representan los coeficientes de la ecuación. Esta forma de la ecuación de una recta permite representar cualquier recta en el plano cartesiano.
La forma punto-pendiente de la ecuación de una recta es y - y1 = m(x - x1), donde m es la pendiente de la recta y (x1, y1) es un punto que pertenece a la recta. Esta forma de la ecuación de una recta permite representar una recta a partir de su pendiente y un punto que pertenece a ella.
Ángulo ConvexoEcuaciones de Curvas
Al igual que las rectas, las curvas en el plano cartesiano pueden ser representadas mediante ecuaciones algebraicas. Existen diferentes tipos de curvas, como círculos, parábolas y elipses, y cada una tiene su propia ecuación característica.
Por ejemplo, la ecuación de un círculo con centro (h, k) y radio r es (x - h)^2 + (y - k)^2 = r^2. Esta ecuación permite representar un círculo en el plano cartesiano a partir de las coordenadas de su centro y su radio.
La ecuación de una parábola en su forma general es y = ax^2 + bx + c, donde a, b y c son constantes. Esta ecuación permite representar una parábola en el plano cartesiano a partir de los coeficientes de la ecuación.
Aplicaciones de la Geometría Analítica
En este apartado se mencionarán algunas aplicaciones de la geometría analítica en diferentes campos, como la física, la ingeniería y la computación.
Física
La geometría analítica tiene diversas aplicaciones en la física, especialmente en el estudio del movimiento de objetos en el espacio. Por ejemplo, se utiliza para describir la trayectoria de un proyectil en un tiro parabólico o para calcular la velocidad y aceleración de un objeto en movimiento.
AnualidadAdemás, la geometría analítica es fundamental en el estudio de la óptica, la mecánica celeste y otras ramas de la física que requieren el análisis de figuras geométricas en el espacio.
Ingeniería
La geometría analítica es ampliamente utilizada en la ingeniería, especialmente en el diseño de estructuras y la resolución de problemas de geometría en la construcción. Por ejemplo, se utiliza para calcular las dimensiones y ángulos de las piezas de una estructura, así como para determinar la ubicación de puntos de interés en un terreno.
Además, la geometría analítica es esencial en la ingeniería de software y la programación, ya que se utiliza en la representación y manipulación de gráficos en 2D y 3D.
Computación
La geometría analítica juega un papel fundamental en la computación, especialmente en la representación y manipulación de gráficos en 2D y 3D. Se utilizan algoritmos y técnicas de geometría analítica para realizar operaciones como la rotación, traslación y escalamiento de objetos en un espacio tridimensional.
Además, la geometría analítica es utilizada en la computación gráfica para la generación de imágenes, la detección de colisiones y la simulación de fenómenos físicos en entornos virtuales.
Ángulos AdyacentesConclusiones
La geometría analítica es una herramienta poderosa que combina el álgebra y la geometría para estudiar las figuras geométricas en el plano cartesiano. Permite representar puntos, rectas y curvas mediante ecuaciones algebraicas, y tiene aplicaciones en diversos campos como la física, la ingeniería y la computación.
La geometría analítica ha evolucionado a lo largo de los siglos, desde los primeros trabajos de René Descartes hasta su desarrollo actual. Ha sido utilizada por matemáticos y científicos para resolver problemas complejos y describir fenómenos naturales.
Referencias
- Descartes, R. (1637). La Géométrie.
- Stewart, J. (2008). Calculus: Early Transcendentals. Cengage Learning.
- Simmons, G. F. (1995). Precalculus Mathematics in a Nutshell: Geometry, Algebra, Trigonometry. Wipf and Stock Publishers.
También te puede interesar: