Hipérbola

Exploraremos en detalle qué es una hipérbola, sus elementos principales y cómo se grafica. La hipérbola es una figura geométrica que tiene propiedades únicas y se utiliza en diversos campos, como la física, la ingeniería y las matemáticas. Comenzaremos por definir qué es una hipérbola y luego analizaremos cada uno de sus elementos.

Definición de hipérbola

Una hipérbola se define como el conjunto de puntos en el plano tales que la diferencia de sus distancias a dos puntos fijos, llamados focos, es constante. Esta diferencia constante se conoce como la distancia focal de la hipérbola. La hipérbola tiene dos ramas simétricas que se extienden infinitamente en dirección opuesta.

Elementos de una hipérbola

Focos

Los focos son los dos puntos fijos que determinan la hipérbola. La distancia entre los focos se denota como 2c. Los focos son esenciales para definir la forma y la posición de la hipérbola.

Centro

El centro de la hipérbola es el punto medio entre los dos focos y se denota como C. El centro es el punto de simetría de la hipérbola y es útil para trazar los ejes y las asíntotas.

Vértices

Los vértices son los puntos de la hipérbola que se encuentran en el eje focal. Hay dos vértices, V1 y V2, que se encuentran a una distancia a del centro. Los vértices son puntos importantes para determinar la forma y la orientación de la hipérbola.

Eje focal

El eje focal es la recta que pasa por los dos focos y el centro de la hipérbola. En una hipérbola, el eje focal puede ser horizontal o vertical. El eje focal es esencial para trazar las asíntotas y determinar la orientación de la hipérbola.

Semieje real

El semieje real es la mitad de la distancia entre los dos vértices y se denota como a. El semieje real determina la amplitud de la hipérbola en la dirección del eje focal.

Semieje imaginario

El semieje imaginario es la mitad de la distancia entre los dos puntos en el eje focal que intersectan la hipérbola y se denota como b. El semieje imaginario determina la amplitud de la hipérbola en la dirección perpendicular al eje focal.

Distancia focal

La distancia focal es la distancia entre el centro y uno de los focos y se denota como c. La distancia focal es importante para determinar la posición de la hipérbola en el plano.

Asíntotas

Las asíntotas son las rectas que se acercan cada vez más a la hipérbola a medida que se alejan del centro. Las ecuaciones de las asíntotas son de la forma y = ±(b/a)x. Las asíntotas son útiles para trazar la forma general de la hipérbola y determinar su comportamiento asintótico.

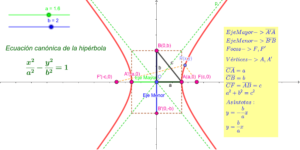
Ecuación canónica de una hipérbola

La ecuación canónica de una hipérbola con centro en el origen y eje focal horizontal es (x^2/a^2) - (y^2/b^2) = 1. Si el eje focal es vertical, la ecuación canónica es (-x^2/a^2) + (y^2/b^2) = 1. Estas ecuaciones permiten representar la forma general de una hipérbola y determinar sus características principales.

Ejemplos de hipérbolas

A continuación, se presentan algunos ejemplos de hipérbolas y cómo se pueden graficar utilizando los elementos mencionados anteriormente:

Ejemplo 1: Graficar la hipérbola con centro en el origen, focos en (0, ±3) y vértices en (±4, 0).
Ejemplo 2: Graficar la hipérbola con centro en (2, -1), focos en (2, 2) y (-2, -1), y vértices en (4, -1) y (0, -1).
Ejemplo 3: Graficar la hipérbola con centro en el origen, focos en (0, ±2) y vértices en (±3, 0).

En cada ejemplo, se utilizarán los elementos de la hipérbola, como los focos, los vértices y la distancia focal, para trazar la forma y la posición de la hipérbola en el plano.

Conclusión

La hipérbola es una figura geométrica con propiedades únicas y una amplia gama de aplicaciones en diversos campos. Sus elementos principales, como los focos, el centro, los vértices y las asíntotas, son fundamentales para comprender y graficar una hipérbola. La ecuación canónica de una hipérbola proporciona una forma general para representar y analizar esta figura geométrica. Al comprender los conceptos y elementos de la hipérbola, podemos utilizarla de manera efectiva en problemas y situaciones del mundo real.