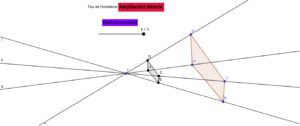
Exploraremos en detalle el concepto de homotecia en geometría. Veremos qué es la homotecia, cómo se define y cómo se aplica en la transformación de figuras geométricas. También analizaremos ejemplos para comprender mejor este concepto.
2. Definición de Homotecia
La homotecia es una correspondencia entre figuras geométricas en la que los puntos correspondientes se encuentran alineados en un punto fijo llamado centro. En una homotecia, los puntos homotéticos se obtienen multiplicando las distancias por un factor común.
2.1 Centro de Homotecia
El centro de homotecia es el punto fijo alrededor del cual se realiza la transformación. Es el único punto que no varía durante la homotecia.
2.2 Factor de Homotecia
El factor de homotecia es el número que se utiliza para multiplicar las distancias y obtener los puntos homotéticos. Este factor determina el cambio de tamaño de la figura.
2.3 Homotecia Directa e Inversa
La homotecia puede ser directa o inversa, dependiendo del valor del factor de homotecia. En una homotecia directa, el factor de homotecia es mayor que 0, lo que significa que la figura se amplía. En una homotecia inversa, el factor de homotecia es menor que 0, lo que significa que la figura se reduce.
3. Propiedades de la Homotecia
La homotecia tiene varias propiedades importantes que debemos tener en cuenta:
3.1 Semejanza
La homotecia permite generar figuras semejantes, es decir, figuras que tienen la misma forma pero difieren en tamaño. Sin embargo, las figuras homotéticas no son congruentes, ya que no tienen la misma forma y tamaño.
3.2 Conservación de la Razón de Lados
En una homotecia, la razón de los lados de la figura original se conserva en la figura homotética. Esto significa que los lados de la figura homotética son proporcionales a los lados de la figura original.
3.3 Conservación de los Ángulos
En una homotecia, los ángulos de la figura original y la figura homotética tienen el mismo valor. Esto significa que los ángulos de la figura homotética son congruentes a los ángulos correspondientes de la figura original.
3.4 Rectas Paralelas y Rectas Dobles
Las rectas que pasan por el centro de homotecia se convierten en rectas dobles en la figura homotética. Esto significa que cada recta que pasa por el centro de homotecia se representa como dos rectas paralelas en la figura homotética. Las rectas que no pasan por el centro de homotecia se convierten en rectas paralelas en la figura homotética.
4. Aplicaciones de la Homotecia
La homotecia tiene varias aplicaciones en la geometría y otras áreas:
4.1 Proyección de Figuras Afines
La homotecia se utiliza en la proyección de figuras afines, donde se transforma una figura en otra figura similar pero de tamaño diferente.
4.2 Diseño y Arquitectura
La homotecia se utiliza en el diseño y la arquitectura para crear modelos a escala de edificios y estructuras.
4.3 Mapas y Cartografía
La homotecia se utiliza en la cartografía para representar mapas y planos a diferentes escalas.
5. Ejemplos de Homotecia
A continuación, se presentan algunos ejemplos para ilustrar cómo funciona la homotecia:
5.1 Ejemplo 1: Homotecia Directa
Consideremos un triángulo ABC y su homotético A’B’C’ con un factor de homotecia de 2. Esto significa que los puntos homotéticos se obtienen multiplicando las distancias por 2. El triángulo A’B’C’ será dos veces más grande que el triángulo ABC, pero conservará la misma forma y proporciones.
5.2 Ejemplo 2: Homotecia Inversa
Consideremos un círculo de radio 5 y su homotético con un factor de homotecia de -0.5. Esto significa que el círculo homotético será la mitad de grande que el círculo original. Además, estará invertido, es decir, estará reflejado con respecto al centro de homotecia.
5.3 Ejemplo 3: Homotecia y Rectas Paralelas
Consideremos un cuadrado ABCD y su homotético A’B’C’D’ con un factor de homotecia de 3. En este caso, las rectas que pasan por el centro de homotecia (el punto de intersección de las diagonales del cuadrado) se convierten en rectas dobles en el cuadrado homotético. Las rectas que no pasan por el centro de homotecia se convierten en rectas paralelas.
6. Conclusiones
La homotecia es una transformación geométrica que permite generar figuras semejantes pero no congruentes. Es útil en la proyección de figuras afines y tiene aplicaciones en el diseño, la arquitectura y la cartografía. La homotecia conserva la razón de los lados y los ángulos de la figura original, y convierte las rectas que pasan por el centro de homotecia en rectas dobles en la figura homotética.