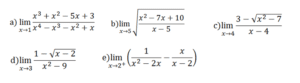Límites Matemáticos – Conceptualista

En matemáticas, los límites son una herramienta fundamental para estudiar el comportamiento de una función o sucesión cuando sus parámetros se acercan a un cierto valor. Exploraremos la definición de límites matemáticos, sus propiedades y ejemplos para comprender mejor su aplicación en el cálculo.

Los límites matemáticos son una parte esencial del cálculo y se utilizan para analizar el comportamiento de una función o sucesión en puntos específicos o en el infinito. Los límites nos permiten determinar cómo se comporta una función o sucesión a medida que sus variables se acercan a un valor determinado. Esto es especialmente útil cuando se trabaja con funciones que no están definidas en ciertos puntos o cuando se desea estudiar el comportamiento de una función en el infinito.

Definición de Límites Matemáticos

Los límites matemáticos se refieren a la magnitud a la que se acercan progresivamente los términos de una secuencia infinita de magnitudes. Formalmente, se dice que el límite de una función f(x) cuando x tiende a un valor c es L si para cualquier ε > 0, existe un δ > 0 tal que si 0 < |x - c| < δ, entonces |f(x) - L| < ε.

En otras palabras, esto significa que podemos hacer que los valores de f(x) se acerquen tanto como queramos a L, siempre y cuando x esté suficientemente cerca de c. La definición de límites matemáticos se basa en la idea de que podemos acercarnos cada vez más a un valor determinado sin llegar a alcanzarlo.

Por ejemplo, si tenemos una función f(x) = x^2 y queremos encontrar el límite de f(x) cuando x tiende a 2, podemos evaluar la función en valores cercanos a 2. Si evaluamos f(x) para x = 1.9, obtenemos f(1.9) = (1.9)^2 = 3.61. Si evaluamos f(x) para x = 2.1, obtenemos f(2.1) = (2.1)^2 = 4.41. Podemos observar que a medida que nos acercamos a x = 2, los valores de f(x) se acercan a 4. Por lo tanto, podemos concluir que el límite de f(x) cuando x tiende a 2 es 4.

Propiedades de los Límites Matemáticos

Los límites matemáticos cumplen con ciertas propiedades que nos permiten simplificar los cálculos y analizar el comportamiento de las funciones de manera más eficiente. Algunas de estas propiedades son:

El límite de una constante es la propia constante: lim (c) = c.
El límite de una suma es la suma de los límites: lim (f(x) + g(x)) = lim (f(x)) + lim (g(x)).
El límite de un producto es el producto de los límites: lim (f(x) * g(x)) = lim (f(x)) * lim (g(x)).
El límite de un cociente es el cociente de los límites, siempre y cuando el límite del denominador no sea cero: lim (f(x) / g(x)) = lim (f(x)) / lim (g(x)).
El límite de una función compuesta es la composición de los límites: lim (f(g(x))) = lim (f(g(x))).

Estas propiedades nos permiten simplificar los cálculos de límites y nos ayudan a comprender mejor el comportamiento de las funciones en diferentes situaciones.

Ejemplos de Límites Matemáticos

Límite de una Función Polinómica

Consideremos la función f(x) = 2x^2 – 3x + 1. Para encontrar el límite de f(x) cuando x tiende a 2, podemos evaluar la función en valores cercanos a 2. Por ejemplo, si evaluamos f(x) para x = 1.9, obtenemos f(1.9) = 2(1.9)^2 – 3(1.9) + 1 = 5.61. Si evaluamos f(x) para x = 2.1, obtenemos f(2.1) = 2(2.1)^2 – 3(2.1) + 1 = 6.61. Podemos observar que a medida que nos acercamos a x = 2, los valores de f(x) se acercan a 6. Por lo tanto, podemos concluir que el límite de f(x) cuando x tiende a 2 es 6.

Límite de una Función Trigonométrica

Consideremos la función g(x) = sin(x) / x. Para encontrar el límite de g(x) cuando x tiende a 0, podemos evaluar la función en valores cercanos a 0. Por ejemplo, si evaluamos g(x) para x = 0.1, obtenemos g(0.1) = sin(0.1) / 0.1 = 0.9983. Si evaluamos g(x) para x = 0.01, obtenemos g(0.01) = sin(0.01) / 0.01 = 0.9998. Podemos observar que a medida que nos acercamos a x = 0, los valores de g(x) se acercan a 1. Por lo tanto, podemos concluir que el límite de g(x) cuando x tiende a 0 es 1.

Límite de una Sucesión

Consideremos la sucesión a_n = 1/n. Para encontrar el límite de la sucesión cuando n tiende a infinito, podemos evaluar los términos de la sucesión para valores grandes de n. Por ejemplo, si evaluamos a_n para n = 10, obtenemos a_10 = 1/10 = 0.1. Si evaluamos a_n para n = 100, obtenemos a_100 = 1/100 = 0.01. Podemos observar que a medida que n tiende a infinito, los términos de la sucesión se acercan a cero. Por lo tanto, podemos concluir que el límite de la sucesión a_n cuando n tiende a infinito es 0.

Conclusiones

Los límites matemáticos son una herramienta esencial en el cálculo y nos permiten estudiar el comportamiento de funciones y sucesiones. A través de la definición formal y las propiedades de los límites, podemos realizar cálculos precisos y comprender mejor el comportamiento de las magnitudes en situaciones límite. Los ejemplos presentados en este artículo ilustran la aplicación de los límites en diferentes contextos matemáticos. Es importante practicar con más ejemplos y ejercicios para fortalecer nuestra comprensión de los límites matemáticos.