Exploraremos en detalle el concepto de líneas paralelas. Veremos qué son, cómo se definen y cuáles son sus características principales. También analizaremos las condiciones necesarias para determinar si dos líneas son paralelas y proporcionaremos ejemplos para una mejor comprensión.
Definición de Líneas Paralelas
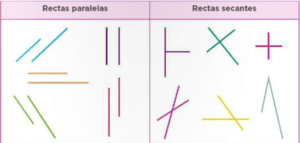
Las líneas paralelas son dos rectas que nunca se tocan y mantienen la misma distancia entre sí en toda su trayectoria. Estas líneas se caracterizan por ser equidistantes y apuntar en la misma dirección.
Características de las Líneas Paralelas
Las líneas paralelas tienen las siguientes características:
- Las líneas nunca se cruzan o se tocan.
- Mantienen la misma distancia entre sí en todos los puntos.
- Apuntan en la misma dirección.
- Las líneas paralelas se extienden hasta el infinito en ambas direcciones.
Estas características hacen que las líneas paralelas sean muy útiles en diversos campos, como la geometría, la arquitectura y la ingeniería. Por ejemplo, en la construcción de edificios, se utilizan líneas paralelas para asegurar que las estructuras sean rectas y estables.
Ángulos Formados por Líneas Paralelas y una Transversal
Cuando una recta transversal cruza a las líneas paralelas, se forman pares de ángulos iguales. Estos ángulos se conocen como ángulos correspondientes, ángulos interiores alternos y ángulos interiores consecutivos.
Ángulos Correspondientes
Los ángulos correspondientes son aquellos que se encuentran en el mismo lado de la transversal y en posiciones correspondientes respecto a las líneas paralelas. Estos ángulos son iguales entre sí.
Por ejemplo, si tenemos dos líneas paralelas y una transversal que las cruza, los ángulos correspondientes serían los ángulos 1 y 5, los ángulos 2 y 6, los ángulos 3 y 7, y los ángulos 4 y 8.
Ángulos Interiores Alternos
Los ángulos interiores alternos son aquellos que se encuentran en el interior de las líneas paralelas y en lados opuestos de la transversal. Estos ángulos son iguales entre sí.
Por ejemplo, si tenemos dos líneas paralelas y una transversal que las cruza, los ángulos interiores alternos serían los ángulos 3 y 6, y los ángulos 4 y 5.
Ángulos Interiores Consecutivos
Los ángulos interiores consecutivos son aquellos que se encuentran en el interior de las líneas paralelas y en el mismo lado de la transversal. La suma de estos ángulos es siempre igual a 180 grados.
Por ejemplo, si tenemos dos líneas paralelas y una transversal que las cruza, los ángulos interiores consecutivos serían los ángulos 3 y 5, y los ángulos 4 y 6. La suma de los ángulos 3 y 5 es igual a 180 grados, al igual que la suma de los ángulos 4 y 6.
Condiciones para Determinar si Dos Líneas son Paralelas
Para comprobar si dos líneas son paralelas, se deben cumplir las siguientes condiciones:
- Los ángulos correspondientes son iguales.
- Los ángulos interiores alternos son iguales.
- Los ángulos interiores consecutivos suman 180 grados.
Si se cumplen estas condiciones, podemos afirmar que las dos líneas son paralelas. De lo contrario, no son paralelas.
Ejemplos de Líneas Paralelas
A continuación, se presentan algunos ejemplos de líneas paralelas:
- Las vías de un tren paralelas entre sí.
- Las líneas de un cuaderno o papel cuadriculado.
- Las líneas de un campo de fútbol.
Estos ejemplos ilustran cómo las líneas paralelas se encuentran en diferentes contextos y son utilizadas en diversas situaciones.
Conclusiones
Las líneas paralelas son rectas que nunca se tocan y mantienen la misma distancia entre sí en toda su trayectoria. Se caracterizan por ser equidistantes y apuntar en la misma dirección. Al cruzarse con una recta transversal, se forman pares de ángulos iguales. Para determinar si dos líneas son paralelas, se deben cumplir ciertas condiciones en relación a los ángulos correspondientes, interiores alternos y consecutivos.