Ojiva

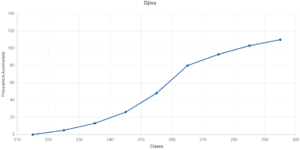
La ojiva en estadística es una herramienta que permite visualizar la distribución de frecuencias de un conjunto de datos. A través de un gráfico de líneas, se muestra la acumulación de frecuencias en función de los valores de los datos. Esto permite analizar la ubicación de los diferentes valores en relación a ciertos parámetros y obtener una representación visual de la distribución de los datos.

Exploraremos en detalle qué es una ojiva, cómo se construye y daremos algunos ejemplos para una mejor comprensión.

¿Qué es una ojiva en estadística?

Una ojiva en estadística es una representación gráfica que muestra la acumulación de frecuencias en función de los valores de los datos. También conocida como polígono de frecuencias acumuladas, la ojiva permite observar la distribución de los datos y analizar la ubicación de los diferentes valores en relación a ciertos parámetros.

Características de una ojiva

• Representación gráfica de la distribución de frecuencias.
• Muestra la acumulación de frecuencias en función de los valores de los datos.
• Puede tener pendiente positiva o pendiente negativa.
• Permite analizar la ubicación de los diferentes valores en relación a ciertos parámetros.

La ojiva es una herramienta útil para analizar la distribución de los datos y obtener una representación visual de cómo se agrupan las frecuencias en función de los valores.

¿Cómo se construye una ojiva?

Para construir una ojiva, se deben seguir los siguientes pasos:

Lee TambiénMultiplicidad

1. Organizar los datos

El primer paso para construir una ojiva es organizar los datos en una tabla. Se deben indicar los valores y sus respectivas frecuencias.

2. Calcular las frecuencias acumuladas

El siguiente paso es calcular las frecuencias acumuladas. Esto implica sumar las frecuencias de los valores anteriores y el valor actual. Las frecuencias acumuladas representan la acumulación de las frecuencias a medida que avanzamos en los valores de los datos.

3. Calcular las frecuencias relativas acumuladas

Una vez calculadas las frecuencias acumuladas, se deben calcular las frecuencias relativas acumuladas. Estas se obtienen dividiendo las frecuencias acumuladas entre el total de datos. Las frecuencias relativas acumuladas representan la proporción acumulada de las frecuencias en relación al total de datos.

4. Representar gráficamente

Finalmente, se representa gráficamente las frecuencias relativas acumuladas en función de los valores de los datos. Se traza una línea que une los puntos correspondientes a cada valor. El resultado es un gráfico de líneas que muestra la acumulación de frecuencias en función de los valores de los datos.

Ejemplo de ojiva

Para entender mejor cómo se construye una ojiva, veamos un ejemplo:

Lee TambiénIsometría

Supongamos que tenemos los siguientes datos:

Valor	Frecuencia
10	3
20	5
30	8
40	6
50	4

Calculamos las frecuencias acumuladas:

Valor	Frecuencia	Frecuencia Acumulada
10	3	3
20	5	8
30	8	16
40	6	22
50	4	26

Calculamos las frecuencias relativas acumuladas:

Valor	Frecuencia	Frecuencia Acumulada	Frecuencia Relativa Acumulada
10	3	3	0.115
20	5	8	0.308
30	8	16	0.615
40	6	22	0.846
50	4	26	1

Representamos gráficamente las frecuencias relativas acumuladas:

Lee TambiénGeometría Euclidiana

En el gráfico de ojiva, podemos observar cómo se acumulan las frecuencias a medida que avanzamos en los valores de los datos. Podemos ver que a medida que aumenta el valor, la frecuencia acumulada también aumenta. Esto nos da una idea de la distribución de los datos y nos permite analizar la ubicación de los diferentes valores en relación a ciertos parámetros.

Conclusiones

La ojiva en estadística es una herramienta útil para visualizar la distribución de frecuencias de un conjunto de datos. Permite analizar la ubicación de los diferentes valores en relación a ciertos parámetros y obtener una representación visual de la distribución de los datos. A través de la construcción de una ojiva, es posible identificar tendencias y patrones en los datos, lo que facilita el análisis estadístico.