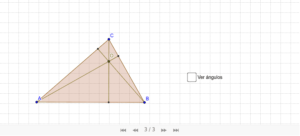
El ortocentro de un triángulo es un punto especial que se encuentra en la intersección de las tres alturas del triángulo. Exploraremos las propiedades del ortocentro y cómo calcular su ubicación en función de las características del triángulo.
Definición del ortocentro
El ortocentro de un triángulo es el punto donde se intersectan las tres alturas del triángulo. Una altura es una recta que pasa por un vértice del triángulo y es perpendicular al lado opuesto.
Ubicación del ortocentro
La ubicación del ortocentro depende de las características del triángulo:
- En un triángulo obtusángulo, el ortocentro se encuentra fuera de la figura.
- En un triángulo rectángulo, el ortocentro coincide con el vértice del ángulo recto.
- En un triángulo acutángulo, el ortocentro se encuentra dentro de la figura.
Cálculo del ortocentro
Para calcular el ortocentro de un triángulo, se deben encontrar las ecuaciones de las tres alturas y resolver el sistema de ecuaciones resultante. Esto se puede hacer utilizando las coordenadas de los vértices del triángulo.
1. Obtención de las ecuaciones de las alturas
Para obtener las ecuaciones de las alturas, se deben seguir los siguientes pasos:
- Seleccionar un vértice del triángulo.
- Encontrar la ecuación de la recta que pasa por ese vértice y es perpendicular al lado opuesto.
- Repetir los pasos 1 y 2 para los otros dos vértices del triángulo.
Por ejemplo, consideremos un triángulo con vértices A(x1, y1), B(x2, y2) y C(x3, y3). Para encontrar la ecuación de la altura que pasa por el vértice A, debemos encontrar la pendiente de la recta que pasa por A y es perpendicular al lado BC. La pendiente de la recta BC se puede calcular utilizando la fórmula:
m = (y2 – y3) / (x2 – x3)
La pendiente de la recta perpendicular a BC se puede calcular como el negativo inverso de la pendiente de BC:
m_perpendicular = -1 / m
La ecuación de la recta que pasa por A y tiene pendiente m_perpendicular se puede escribir como:
y – y1 = m_perpendicular * (x – x1)
Repetimos este proceso para los otros dos vértices del triángulo para obtener las ecuaciones de las otras dos alturas.
2. Resolución del sistema de ecuaciones
Una vez obtenidas las ecuaciones de las tres alturas, se debe resolver el sistema de ecuaciones resultante para encontrar las coordenadas del ortocentro.
Por ejemplo, supongamos que las ecuaciones de las tres alturas son:
h1: y – y1 = m1 * (x – x1)
h2: y – y2 = m2 * (x – x2)
h3: y – y3 = m3 * (x – x3)
Para encontrar las coordenadas del ortocentro, debemos resolver el sistema de ecuaciones:
h1 ∩ h2 ∩ h3
Esto se puede hacer utilizando métodos algebraicos, como sustitución o eliminación.
Propiedades del ortocentro
El ortocentro tiene varias propiedades interesantes:
- En un triángulo equilátero, el ortocentro, el circuncentro, el baricentro y el incentro coinciden en un punto interior que está equidistante de los tres vértices.
- En un triángulo no equilátero, el ortocentro, el circuncentro y el baricentro están alineados en la recta de Euler.
- La distancia del ortocentro al baricentro es el doble de la distancia del baricentro al circuncentro.
Relación con el triángulo órtico
El ortocentro está relacionado con el triángulo órtico, que es un triángulo formado por las proyecciones de los vértices del triángulo original sobre los lados opuestos. El incentro del triángulo órtico coincide con el ortocentro del triángulo original.
Conclusión
El ortocentro de un triángulo es el punto donde se intersectan las tres alturas del triángulo. Su ubicación depende de las características del triángulo y se puede calcular encontrando las ecuaciones de las alturas y resolviendo el sistema resultante. El ortocentro tiene propiedades interesantes, como su relación con el circuncentro, el baricentro y el incentro, y su relación con el triángulo órtico.