Exploraremos en detalle el concepto de permutación. Veremos su definición, su concepto matemático, su relación con la combinatoria y su importancia en la teoría de grupos. También proporcionaremos ejemplos para ayudar a comprender mejor este concepto.
Definición de Permutación
La permutación es un concepto que proviene del latín permutatio y se refiere al procedimiento y resultado de intercambiar una cosa por otra sin utilizar dinero. En matemáticas, la permutación se refiere a los posibles ordenamientos de elementos en un conjunto no infinito. Es un cambio en la disposición de los elementos y puede considerarse como una función biyectiva dentro del conjunto.
Concepto de Permutación
En el contexto matemático, la permutación se refiere a los diferentes arreglos u ordenamientos que se pueden hacer con los elementos de un conjunto. Por ejemplo, si tenemos un conjunto de tres elementos: A, B y C, las permutaciones posibles son ABC, ACB, BAC, BCA, CAB y CBA. Cada una de estas permutaciones representa un ordenamiento diferente de los elementos del conjunto.
Las permutaciones se pueden representar de diferentes maneras, como listas, ciclos o notación de dos filas. Cada forma de representación tiene sus propias ventajas y se utiliza en diferentes contextos.
Representación de Permutaciones
Existen varias formas de representar las permutaciones:
- Notación de lista: Se representa la permutación como una lista ordenada de elementos. Por ejemplo, la permutación ABC se representa como [A, B, C].
- Notación de ciclo: Se agrupan los elementos en ciclos de longitud 2. Por ejemplo, la permutación ABC se representa como (AB)(AC)(BC).
- Notación de dos filas: Se representan los elementos del conjunto en dos filas, donde la primera fila muestra los elementos originales y la segunda fila muestra los elementos permutados. Por ejemplo, la permutación ABC se representa como:
| Elementos originales | Elementos permutados |
|---|---|
| A | B |
| B | A |
| C | C |
Permutación y Combinatoria
La permutación está estrechamente relacionada con la combinatoria, que es el estudio de la numeración, existencia y construcción de configuraciones que cumplen ciertas reglas. La combinatoria se ocupa de determinar la cantidad de formas diferentes en las que se pueden considerar conjuntos formados a partir de elementos de un conjunto inicial, siguiendo reglas como el orden, la partición, la repetición y el tamaño.
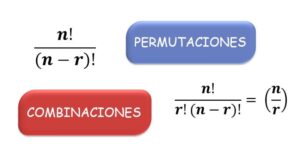
En el caso de las permutaciones, la combinatoria se utiliza para determinar el número total de permutaciones posibles para un conjunto dado. La fórmula para calcular el número de permutaciones de n elementos es n!, donde n es el número de elementos en el conjunto y ! representa el factorial.
Por ejemplo, si tenemos un conjunto de 4 elementos, el número total de permutaciones posibles sería 4! = 4 x 3 x 2 x 1 = 24.
Permutaciones y Transposiciones
Dentro de las permutaciones, existe un tipo especial llamado transposición. Una transposición es una permutación en la que se intercambian dos elementos contiguos. Por ejemplo, si tenemos la permutación ABC, una transposición posible sería intercambiar A y B, lo que resultaría en la permutación BAC.
Cualquier permutación se puede descomponer en ciclos de longitud 2, es decir, en transposiciones. Esto significa que cualquier permutación se puede escribir como un producto de transposiciones y, por lo tanto, de ciclos.
La descomposición de una permutación en ciclos de longitud 2 es única, lo que significa que no importa cómo se descomponga una permutación en transposiciones, el resultado final será el mismo.
Permutaciones y la Teoría de Grupos
El estudio de la permutación de las raíces de ecuaciones algebraicas fue fundamental para el matemático Évariste Galois en el desarrollo de la teoría de grupos. Galois trabajó con grupos no abelianos, que no son conmutativos, y utilizó el término permutaciones en el contexto de las matemáticas.
La teoría de grupos es una rama importante de las matemáticas que estudia las propiedades y estructuras de los conjuntos con una operación binaria. Las permutaciones juegan un papel fundamental en la teoría de grupos, ya que los grupos de permutaciones son un ejemplo importante de grupos no abelianos.
La teoría de grupos tiene aplicaciones en diversos campos, como la criptografía, la física teórica y la teoría de números. El estudio de las permutaciones y su relación con la teoría de grupos ha sido fundamental en el desarrollo de estas áreas de investigación.
Conclusiones
La permutación es el intercambio de una cosa por otra sin utilizar dinero. En matemáticas, se refiere a los posibles ordenamientos de elementos en un conjunto no infinito y está relacionada con la combinatoria. También se pueden descomponer en ciclos de longitud 2 llamados transposiciones. El estudio de las permutaciones fue fundamental en el desarrollo de la teoría de grupos por parte de Évariste Galois.
Las permutaciones tienen aplicaciones en diversos campos de las matemáticas y otras disciplinas, y su estudio es fundamental para comprender la estructura y las propiedades de los conjuntos y grupos.
Ejemplos de Permutaciones
A continuación, se presentan algunos ejemplos de permutaciones:
- Permutaciones de un conjunto de 3 elementos: ABC, ACB, BAC, BCA, CAB, CBA.
- Permutaciones de un conjunto de 4 elementos: ABCD, ABDC, ACBD, ACDB, ADBC, ADCB, BACD, BADC, BCAD, BCDA, BDAC, BDCA, CABD, CADB, CBAD, CBDA, CDAB, CDBA, DABC, DACB, DBAC, DBCA, DCAB, DCBA.
Estos ejemplos ilustran la variedad de permutaciones posibles para conjuntos de diferentes tamaños.