Programación Lineal

La programación lineal es una técnica matemática utilizada para optimizar una función objetivo sujeta a restricciones lineales. Fue desarrollada durante la Segunda Guerra Mundial y ha encontrado aplicaciones en diversos campos, como la economía, la ingeniería y la logística. Exploraremos los conceptos básicos de la programación lineal y cómo se aplica en la resolución de problemas.

Definición de Programación Lineal

La programación lineal es un método matemático que busca maximizar o minimizar una función objetivo lineal, sujeta a un conjunto de restricciones lineales. La función objetivo y las restricciones se expresan en forma de ecuaciones o desigualdades lineales. El objetivo es encontrar los valores de las variables que optimicen la función objetivo, cumpliendo con todas las restricciones establecidas.

Función Objetivo

La función objetivo es una expresión matemática lineal que representa la cantidad que se desea maximizar o minimizar. Puede ser una función de una o varias variables, y su forma general es:

Función Objetivo: Z = c1x1 + c2x2 + ... + cnxn

Donde Z es el valor de la función objetivo, c1, c2, ..., cn son los coeficientes de las variables x1, x2, ..., xn, respectivamente.

Lee TambiénProbabilidad Subjetiva

Restricciones

Las restricciones son condiciones que limitan los valores que pueden tomar las variables en la función objetivo. Estas restricciones se expresan en forma de ecuaciones o desigualdades lineales. Las restricciones típicas incluyen límites de recursos, capacidades de producción o demanda, y restricciones tecnológicas. Las restricciones se pueden representar de la siguiente manera:

Restricción 1: a11x1 + a12x2 + ... + a1nxn ≤ b1

Restricción 2: a21x1 + a22x2 + ... + a2nxn ≤ b2

...

Restricción m: am1x1 + am2x2 + ... + amnxn ≤ bm

Lee TambiénProbabilidad Condicional

Donde aij son los coeficientes de las variables x1, x2, ..., xn en la restricción i, y bi es el límite o valor máximo permitido para la restricción i.

Historia de la Programación Lineal

La programación lineal fue desarrollada durante la Segunda Guerra Mundial por varios matemáticos, entre ellos John von Neumann, George Dantzig y Leonid Kantoróvich. Fue utilizada para gestionar y planificar los gastos del ejército, optimizando la asignación de recursos limitados. Desde entonces, la programación lineal ha evolucionado y se ha convertido en una herramienta fundamental en la toma de decisiones en diversos campos.

Modelos de Programación Lineal

Los modelos de programación lineal se basan en variables de decisión lineales, es decir, variables que se pueden expresar como una combinación lineal de las variables originales. Esto simplifica los cálculos y permite encontrar soluciones óptimas de manera eficiente. Algunos ejemplos de modelos de programación lineal incluyen la asignación de recursos, la planificación de la producción y la optimización de rutas de transporte.

Conceptos Clave en la Programación Lineal

Solución Factible

Una solución factible es un conjunto de valores para las variables que cumple con todas las restricciones del problema. En otras palabras, es un punto dentro del recinto definido por las restricciones. Una solución factible puede no ser óptima, pero es una solución válida.

Solución Óptima

Una solución óptima es aquella que maximiza o minimiza la función objetivo, cumpliendo con todas las restricciones del problema. En la programación lineal, las soluciones óptimas se encuentran en los vértices del recinto definido por las restricciones. Estos vértices representan las combinaciones de valores que optimizan la función objetivo.

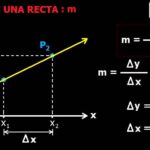Lee TambiénPendiente

Valor del Programa Lineal

El valor del programa lineal es el valor de la función objetivo en el vértice de la solución óptima. Representa el resultado óptimo del problema y puede interpretarse como la cantidad máxima o mínima que se puede alcanzar.

Ejemplo de Programación Lineal

Un ejemplo común de programación lineal es la distribución de una herencia entre acciones y bonos. Supongamos que se desea invertir una cantidad determinada de dinero en acciones y bonos, y se establecen restricciones sobre la cantidad a invertir en cada opción. La función objetivo podría ser maximizar el rendimiento total de la inversión, sujeto a las restricciones de inversión en acciones y bonos. Mediante la programación lineal, se pueden encontrar las cantidades óptimas a invertir en cada opción para maximizar el rendimiento total.

Conclusión

La programación lineal es una técnica matemática poderosa que permite optimizar una función objetivo sujeta a restricciones lineales. Es ampliamente utilizada en la resolución de problemas de optimización en diversos campos. Hemos explorado los conceptos básicos de la programación lineal, incluyendo la definición, las restricciones, los conceptos clave y un ejemplo práctico. Esperamos que esta información te haya ayudado a comprender mejor esta técnica y su aplicación en la resolución de problemas.