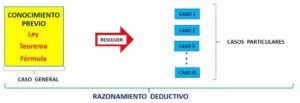
El razonamiento deductivo es un proceso mental que permite inferir una conclusión necesaria a partir de una serie de premisas. Se basa en la deducción, que es el método lógico que va de lo universal a lo particular. Exploraremos las características del razonamiento deductivo, su definición y algunos ejemplos para comprender mejor este tipo de razonamiento.
Características del razonamiento deductivo
- Parte de premisas universales
- Utiliza reglas de inferencia
- Es una secuencia bien definida
- Puede incluir axiomas
- La conclusión es necesaria
- No siempre garantiza la verdad
- No siempre ofrece información detallada
- Puede haber diferentes conclusiones posibles
1. Parte de premisas universales
El razonamiento deductivo comienza con premisas generales o universales que se consideran verdaderas. Estas premisas establecen las bases para el razonamiento y son fundamentales para llegar a una conclusión lógica.
Por ejemplo, si tenemos las premisas «Todos los mamíferos son animales» y «Los perros son mamíferos», podemos inferir la conclusión «Los perros son animales». En este caso, las premisas universales nos permiten llegar a una conclusión específica.
2. Utiliza reglas de inferencia
Para llegar a la conclusión, el razonamiento deductivo utiliza reglas de inferencia o transformación lógica que analizan las premisas y arrojan una o más conclusiones. Estas reglas son fundamentales para garantizar la validez del razonamiento y la coherencia de la conclusión.
Por ejemplo, una regla de inferencia común es el modus ponens, que establece que si tenemos una premisa condicional «Si A, entonces B» y la premisa «A», podemos inferir la conclusión «B». Esta regla nos permite deducir una conclusión a partir de una premisa condicional y una premisa que cumple la condición.
3. Es una secuencia bien definida
El razonamiento deductivo sigue una secuencia lógica y estructurada de fórmulas, donde la última fórmula es la conclusión del argumento. Cada paso en el razonamiento está claramente definido y se basa en las premisas y las reglas de inferencia utilizadas.
Por ejemplo, si tenemos las premisas «Todos los seres humanos son mortales» y «Sócrates es un ser humano», podemos seguir una secuencia lógica para llegar a la conclusión «Sócrates es mortal». Siguiendo las premisas y aplicando la regla de inferencia de la generalización, podemos llegar a la conclusión necesaria.
4. Puede incluir axiomas
En algunos casos, el razonamiento deductivo puede incluir axiomas, que son proposiciones consideradas evidentes y no requieren demostración previa. Estos axiomas son aceptados como verdaderos y se utilizan como base para el razonamiento deductivo.
Por ejemplo, en la geometría euclidiana, se utilizan axiomas como «Dos puntos determinan una línea recta» o «La suma de los ángulos internos de un triángulo es igual a 180 grados». Estos axiomas son considerados verdaderos y se utilizan como base para deducir otras proposiciones geométricas.
5. La conclusión es necesaria
En el razonamiento deductivo, la conclusión se deriva necesariamente de las premisas. Si las premisas son verdaderas y el razonamiento es válido, la conclusión también será verdadera. La conclusión no es una mera posibilidad, sino que se sigue lógicamente de las premisas establecidas.
Por ejemplo, si tenemos las premisas «Todos los gatos son animales» y «Milo es un gato», podemos inferir necesariamente la conclusión «Milo es un animal». Si las premisas son verdaderas, la conclusión también será verdadera.
6. No siempre garantiza la verdad
Aunque el razonamiento deductivo sigue una estructura lógica, no siempre garantiza la verdad de la conclusión. Si las premisas son falsas o la estructura del razonamiento es incorrecta, la conclusión puede ser falsa. Es importante tener en cuenta que la validez del razonamiento deductivo no garantiza la verdad de la conclusión, solo garantiza que si las premisas son verdaderas, la conclusión también lo será.
Por ejemplo, si tenemos las premisas «Todos los pájaros son mamíferos» y «Los perros son pájaros», podemos seguir una secuencia lógica para llegar a la conclusión «Los perros son mamíferos». Sin embargo, esta conclusión es falsa porque las premisas son incorrectas.
7. No siempre ofrece información detallada
Aunque el razonamiento deductivo parte de lo general para llegar a lo particular, no siempre ofrece información detallada o precisa. La conclusión puede ser cierta, pero no proporcionar todos los detalles relevantes. Es posible que se requiera un razonamiento adicional o más información para obtener una comprensión completa de la situación.
Por ejemplo, si tenemos las premisas «Todos los estudiantes son inteligentes» y «Juan es un estudiante», podemos inferir la conclusión «Juan es inteligente». Sin embargo, esta conclusión no nos proporciona información detallada sobre el nivel de inteligencia de Juan o las habilidades específicas que posee.
8. Puede haber diferentes conclusiones posibles
En algunos casos, el razonamiento deductivo puede conducir a diferentes conclusiones posibles, dependiendo de las premisas utilizadas y las reglas de inferencia aplicadas. Esto puede ocurrir cuando las premisas son ambiguas o cuando se aplican diferentes reglas de inferencia para llegar a diferentes conclusiones. Es importante evaluar cuidadosamente las premisas y las reglas de inferencia utilizadas para evitar conclusiones erróneas.
Por ejemplo, si tenemos las premisas «Todos los animales tienen cuatro patas» y «Este animal tiene cuatro patas», podemos inferir la conclusión «Este animal es un perro». Sin embargo, también podríamos inferir la conclusión «Este animal es un gato» si tenemos otra premisa que establezca que el animal tiene pelo y ronronea.
Conclusión
El razonamiento deductivo es un proceso mental que parte de premisas universales y utiliza reglas de inferencia para llegar a una conclusión necesaria. Aunque sigue una estructura lógica, no siempre garantiza la verdad de la conclusión y no siempre ofrece información detallada. Es importante aplicar el razonamiento deductivo de manera cuidadosa y crítica, evaluando las premisas y las reglas de inferencia utilizadas para obtener conclusiones válidas y coherentes.