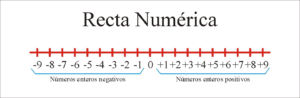
La recta numérica es una herramienta fundamental en matemáticas que nos permite representar y comprender los números de manera visual y ordenada. Exploraremos la utilidad de la recta numérica y cómo se utiliza en diferentes contextos matemáticos.
La recta numérica es una línea recta en la que se representan los números de manera ordenada. En ella, cada punto corresponde a un número específico y se coloca de acuerdo a su posición relativa en relación a otros números. La recta numérica se extiende infinitamente en ambas direcciones y se divide en segmentos iguales, generalmente representados por unidades.
Utilidad de la recta numérica
1. Representación de números enteros
La recta numérica es especialmente útil para representar y comprender los números enteros. En ella, los números enteros se colocan en la recta de acuerdo a su valor absoluto y su relación de orden. Por ejemplo, el número 0 se coloca en el centro de la recta, los números positivos se ubican a la derecha del 0 y los números negativos se ubican a la izquierda del 0.
Por ejemplo, si queremos representar los números enteros del -3 al 3 en la recta numérica, colocamos el número -3 a la izquierda del 0, el número -2 a la izquierda del -3, y así sucesivamente hasta llegar al número 3 a la derecha del 0. De esta manera, podemos visualizar y comprender la relación de orden entre los números enteros.
2. Comparación de números
La recta numérica nos permite visualizar y comparar fácilmente los números. Al observar la posición de dos números en la recta, podemos determinar cuál es mayor o menor. Por ejemplo, si tenemos los números -3 y 2, podemos ver que 2 está a la derecha de -3, por lo tanto, 2 es mayor que -3.
Además, la recta numérica nos permite determinar la distancia entre dos números. Por ejemplo, si queremos determinar la distancia entre -3 y 2, simplemente contamos los segmentos entre los dos números en la recta numérica. En este caso, la distancia es de 5 segmentos.
3. Representación de fracciones
La recta numérica también se utiliza para representar fracciones. En este caso, se divide la recta en segmentos iguales que representan las unidades y se colocan los puntos correspondientes a las fracciones en su posición relativa. Por ejemplo, si queremos representar la fracción 1/2, la colocamos en el punto medio entre 0 y 1.
De esta manera, podemos visualizar y comprender la relación de orden entre las fracciones. Por ejemplo, si queremos comparar las fracciones 1/4 y 3/4, podemos ver que 3/4 está a la derecha de 1/4 en la recta numérica, por lo tanto, 3/4 es mayor que 1/4.
4. Resolución de problemas de suma y resta
La recta numérica es una herramienta útil para resolver problemas de suma y resta. Al representar los números en la recta, podemos visualizar el proceso de sumar o restar y determinar el resultado de manera más clara. Por ejemplo, si queremos sumar 3 a -2, podemos ubicar -2 en la recta y avanzar 3 unidades hacia la derecha para encontrar el resultado.
De la misma manera, si queremos restar 3 a -2, podemos ubicar -2 en la recta y retroceder 3 unidades hacia la izquierda para encontrar el resultado. La recta numérica nos ayuda a visualizar y comprender el proceso de suma y resta, facilitando la resolución de problemas.
5. Representación gráfica de funciones
En el ámbito de las funciones matemáticas, la recta numérica se utiliza para representar gráficamente las funciones lineales. Al colocar los puntos correspondientes a los valores de x e y en la recta, podemos trazar una línea recta que representa la función. Esto nos permite visualizar la relación entre las variables y analizar el comportamiento de la función.
Por ejemplo, si tenemos la función y = 2x + 1, podemos colocar los puntos correspondientes a los valores de x e y en la recta numérica y trazar una línea recta que pasa por estos puntos. De esta manera, podemos visualizar y comprender la relación entre las variables x e y en la función.
6. Realización de mediciones
La recta numérica también se utiliza en la realización de mediciones. Por ejemplo, si queremos medir la distancia entre dos puntos en una recta, podemos utilizar la recta numérica para determinar la diferencia entre los valores de los puntos y obtener la medida exacta.
Por ejemplo, si queremos medir la distancia entre los puntos -3 y 2 en la recta numérica, simplemente restamos el valor de -3 al valor de 2, obteniendo una distancia de 5 unidades.
Conclusiones
La recta numérica es una herramienta esencial en matemáticas que nos permite representar y comprender los números de manera visual y ordenada. Su utilidad abarca desde la representación de números enteros y fracciones, hasta la resolución de problemas de suma y resta, la representación gráfica de funciones y la realización de mediciones. Dominar el uso de la recta numérica es fundamental para desarrollar habilidades matemáticas sólidas y facilitar la comprensión de conceptos numéricos.