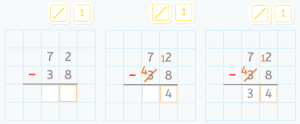
La resta, también conocida como sustracción, es una operación matemática fundamental que nos permite encontrar la diferencia entre dos cantidades. Es la operación inversa a la suma y se utiliza en una amplia variedad de situaciones en la vida cotidiana y en diferentes ramas de las matemáticas.
Exploraremos en detalle la definición, el concepto, el significado y los ejemplos de la resta, así como su aplicación en diferentes contextos.
Definición de la resta
La resta es una operación matemática que consiste en sacar, recortar, empequeñecer, reducir o separar algo de un todo. Se realiza restando el sustraendo del minuendo y el resultado se llama diferencia.
En términos más simples, la resta implica encontrar la cantidad que se debe quitar o separar de una cantidad inicial para obtener una cantidad final deseada.
Concepto de la resta
El concepto de la resta se basa en la idea de quitar o separar una cantidad de otra. Por ejemplo, si tenemos 8 manzanas y le quitamos 3, nos quedan 5 manzanas. En este caso, el número 8 es el minuendo, el número 3 es el sustraendo y el resultado, 5, es la diferencia.
En términos más generales, el minuendo representa la cantidad inicial o total, el sustraendo representa la cantidad que se quita o se separa y la diferencia representa la cantidad que queda después de la resta.
Propiedades de la resta
La resta tiene varias propiedades importantes que debemos tener en cuenta:
- La resta es una operación binaria, es decir, requiere de dos números para realizarse.
- La resta es conmutativa, lo que significa que el orden de los números no afecta al resultado. Por ejemplo, 5 – 3 es igual a 3 – 5.
- La resta es asociativa, lo que significa que el agrupamiento de los números no afecta al resultado. Por ejemplo, (8 – 3) – 2 es igual a 8 – (3 – 2).
- La resta tiene una propiedad de identidad, donde restar cero a cualquier número no cambia su valor. Por ejemplo, 7 – 0 es igual a 7.
Estas propiedades nos permiten realizar operaciones de resta de manera más eficiente y nos ayudan a comprender mejor cómo funciona esta operación matemática.
Resta en diferentes contextos
Resta de números naturales
En el caso de los números naturales, la resta se realiza cuando el minuendo es mayor que el sustraendo. Si el sustraendo es mayor, el resultado será un número negativo. Por ejemplo, si tenemos 8 manzanas y le quitamos 3, nos quedan 5 manzanas. En este caso, 8 es el minuendo, 3 es el sustraendo y 5 es la diferencia.
La resta de números naturales se realiza de manera similar a la resta de números enteros, pero sin la posibilidad de obtener resultados negativos.
Resta de números enteros
En los números enteros, la resta se realiza de manera similar a los números naturales. Sin embargo, en este caso, se pueden obtener resultados negativos incluso cuando el minuendo es mayor que el sustraendo. Por ejemplo, si tenemos -5 manzanas y le quitamos -3 manzanas, nos quedan -2 manzanas. En este caso, -5 es el minuendo, -3 es el sustraendo y -2 es la diferencia.
La resta de números enteros nos permite representar situaciones de deuda, pérdida o disminución en la cantidad de algo.
Resta de números decimales
La resta de números decimales se realiza de la misma manera que la resta de números enteros. Se alinean los números decimales y se realiza la resta como de costumbre. Por ejemplo, si tenemos 3.5 y le restamos 1.2, el resultado es 2.3.
La resta de números decimales se utiliza en situaciones que involucran mediciones precisas, como en ciencias, ingeniería o finanzas.
Resta de fracciones
La resta de fracciones requiere pasos adicionales para encontrar una solución compatible. Se deben encontrar un denominador común y luego restar los numeradores. Por ejemplo, si tenemos 3/4 y le restamos 1/2, el resultado es 1/4.
La resta de fracciones se utiliza en situaciones que involucran partes de un todo, como en recetas de cocina, repartición de recursos o cálculos de probabilidades.
Resta de vectores
En física y geometría, la resta de vectores se utiliza para encontrar la diferencia entre dos vectores. Se restan las componentes correspondientes de los vectores y se obtiene un nuevo vector resultante. Por ejemplo, si tenemos un vector A = (3, 2) y un vector B = (1, 1), la resta de A – B es igual a (2, 1).
La resta de vectores se utiliza para representar desplazamientos, fuerzas o velocidades en diferentes direcciones y magnitudes.
Ejemplos de resta
Para comprender mejor cómo se realiza la resta, veamos algunos ejemplos:
Ejemplo 1
Resta de números naturales: 8 – 3 = 5
En este ejemplo, tenemos 8 manzanas y le quitamos 3 manzanas. Nos quedan 5 manzanas.
Ejemplo 2
Resta de números enteros: -5 – (-3) = -2
En este ejemplo, tenemos -5 manzanas y le quitamos -3 manzanas. Nos quedan -2 manzanas.
Ejemplo 3
Resta de números decimales: 3.5 – 1.2 = 2.3
En este ejemplo, tenemos 3.5 y le restamos 1.2. El resultado es 2.3.
Ejemplo 4
Resta de fracciones: 3/4 – 1/2 = 1/4
En este ejemplo, tenemos 3/4 y le restamos 1/2. El resultado es 1/4.
Ejemplo 5
Resta de vectores: A = (3, 2) y B = (1, 1), A – B = (2, 1)
En este ejemplo, tenemos un vector A con componentes (3, 2) y un vector B con componentes (1, 1). Restamos las componentes correspondientes y obtenemos un nuevo vector resultante con componentes (2, 1).
Conclusión
La resta es una operación matemática esencial que nos permite encontrar la diferencia entre dos cantidades. Se utiliza en una amplia variedad de situaciones y contextos, desde números naturales hasta vectores en física y geometría. Es importante comprender los conceptos y propiedades de la resta para poder aplicarla correctamente en diferentes situaciones.