Resta De Vectores

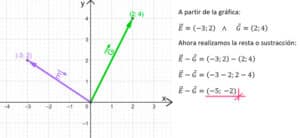
La resta de vectores es una operación matemática que permite calcular la diferencia entre dos vectores. Esta operación es fundamental en el estudio de los vectores y se utiliza en diversos campos como la física, la geometría y la ingeniería.

Exploraremos en detalle qué es la resta de vectores, cómo se realiza, sus propiedades y algunas aplicaciones prácticas. Además, proporcionaremos ejemplos para ayudar a comprender mejor este concepto.

Definición de la resta de vectores

La resta de vectores se realiza restando las componentes correspondientes de los vectores. Para restar dos vectores, se restan las componentes correspondientes de cada vector y se obtiene un nuevo vector resultante.

Ejemplo

Si tenemos dos vectores A y B, la resta de estos vectores se calcula restando las componentes correspondientes: A - B = (Ax - Bx, Ay - By).

En este ejemplo, restamos las componentes x y y de los vectores A y B para obtener un nuevo vector resultante.

Propiedades de la resta de vectores

La resta de vectores tiene las siguientes propiedades:

La resta de vectores es una operación conmutativa, es decir, el orden en que se restan los vectores no afecta al resultado final. A - B = B - A.
La resta de vectores es una operación asociativa, es decir, el resultado de restar tres vectores es el mismo independientemente del orden en que se realicen las restas. (A - B) - C = A - (B - C).
La resta de un vector consigo mismo da como resultado el vector nulo. A - A = 0.

Estas propiedades son importantes para simplificar cálculos y demostraciones en el estudio de los vectores.

Aplicaciones de la resta de vectores

La resta de vectores se utiliza en diversas aplicaciones, entre las que se incluyen:

En física, la resta de vectores se utiliza para calcular la velocidad relativa entre dos objetos en movimiento. Por ejemplo, si tenemos un objeto A que se mueve a una velocidad de 5 m/s hacia el este y un objeto B que se mueve a una velocidad de 3 m/s hacia el oeste, podemos restar estos vectores para obtener la velocidad relativa entre los dos objetos.
En geometría, la resta de vectores se utiliza para calcular la dirección y magnitud de un vector resultante. Por ejemplo, si tenemos dos vectores A y B que representan fuerzas aplicadas a un objeto, podemos restar estos vectores para obtener la fuerza resultante que actúa sobre el objeto.
En ingeniería, la resta de vectores se utiliza para calcular fuerzas resultantes en sistemas de fuerzas. Por ejemplo, si tenemos varias fuerzas aplicadas a un objeto en diferentes direcciones, podemos restar estos vectores para obtener la fuerza resultante que actúa sobre el objeto.

Estas son solo algunas de las muchas aplicaciones de la resta de vectores en diferentes campos. Esta operación es de gran utilidad para el análisis y la resolución de problemas en estas áreas.

Conclusiones

La resta de vectores es una operación matemática fundamental en el estudio de los vectores. Permite calcular la diferencia entre dos vectores y se utiliza en diversos campos como la física, la geometría y la ingeniería. La resta de vectores se realiza restando las componentes correspondientes de los vectores y tiene propiedades como la conmutatividad y la asociatividad. Esta operación es de gran utilidad para el análisis y la resolución de problemas en estas áreas.