Exploraremos la definición formal de un tensor, su importancia en matemáticas y física, y algunos ejemplos para comprender mejor este concepto fundamental.
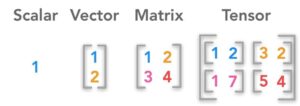
Un tensor es un objeto algebraico que describe una relación multilineal entre conjuntos de objetos algebraicos relacionados con un espacio vectorial. Puede mapear vectores, escalares e incluso otros tensores. Los tensores se definen independientemente de cualquier base y se pueden representar como matrices multidimensionales. También se pueden definir como mapas multilineales utilizando productos tensoriales. Los componentes de un tensor se transforman de acuerdo con las leyes de transformación covariantes y contravariantes. Los tensores son importantes en física porque proporcionan un marco matemático para resolver problemas en áreas como la mecánica, la electrodinámica y la relatividad general. En algunas aplicaciones, los tensores pueden variar en cada punto de un objeto, lo que lleva al concepto de campo tensorial.
¿Qué es un tensor?
Un tensor es un objeto algebraico que describe una relación multilineal entre conjuntos de objetos algebraicos relacionados con un espacio vectorial. Puede mapear vectores, escalares e incluso otros tensores. Los tensores se definen independientemente de cualquier base y se pueden representar como matrices multidimensionales. También se pueden definir como mapas multilineales utilizando productos tensoriales.
Definición matemática
Matemáticamente, un tensor se define independientemente de cualquier base y se puede representar como matrices multidimensionales. Un tensor de rango n se representa como una matriz de n índices. Cada índice puede tomar valores en un conjunto de números, generalmente enteros, que representan las dimensiones del tensor. Por ejemplo, un tensor de rango 2 se representa como una matriz bidimensional.
Los tensores también se pueden definir como mapas multilineales utilizando productos tensoriales. Un producto tensorial es una operación que combina dos tensores para formar un nuevo tensor. El producto tensorial se define de manera que los componentes del tensor resultante se obtienen multiplicando los componentes correspondientes de los tensores de entrada.
Transformación de componentes
Los componentes de un tensor se transforman de acuerdo con las leyes de transformación covariantes y contravariantes. Esto significa que los componentes de un tensor cambian cuando se cambia el sistema de coordenadas utilizado para describir el espacio vectorial. Las leyes de transformación covariantes y contravariantes aseguran que las relaciones entre los componentes de un tensor se mantengan invariantes bajo cambios de coordenadas.
La transformación de componentes de un tensor se puede describir utilizando matrices de transformación. Estas matrices representan las relaciones entre los sistemas de coordenadas antes y después de la transformación. Al aplicar la matriz de transformación a los componentes del tensor, se obtienen los nuevos componentes en el nuevo sistema de coordenadas.
Importancia de los tensores en física
Los tensores son fundamentales en física porque proporcionan un marco matemático para resolver problemas en áreas como la mecánica, la electrodinámica y la relatividad general. Los tensores permiten describir y analizar fenómenos físicos complejos de manera precisa y rigurosa.
Aplicaciones en mecánica
En mecánica, los tensores se utilizan para describir el comportamiento elástico de materiales, como la deformación de un sólido bajo la aplicación de fuerzas externas. Los tensores de deformación y esfuerzo se utilizan para caracterizar cómo se distribuyen las fuerzas internas en un material y cómo se deforma en respuesta a estas fuerzas.
Los tensores también se utilizan para describir el movimiento de objetos en el espacio tridimensional. Por ejemplo, el tensor de inercia se utiliza para describir cómo se distribuye la masa de un objeto y cómo resiste los cambios en su movimiento.
Aplicaciones en electrodinámica
En electrodinámica, los tensores se utilizan para describir el campo electromagnético y las interacciones entre cargas eléctricas y corrientes. El tensor del campo electromagnético combina las componentes del campo eléctrico y magnético en un solo objeto matemático que describe completamente el campo electromagnético en un punto dado del espacio y tiempo.
Los tensores también se utilizan para describir las ecuaciones de Maxwell, que son las ecuaciones fundamentales que gobiernan el comportamiento de los campos eléctricos y magnéticos. Estas ecuaciones relacionan las derivadas espaciales y temporales de los campos con las fuentes de carga y corriente.
Aplicaciones en relatividad general
En relatividad general, los tensores se utilizan para describir la geometría del espacio-tiempo y las ecuaciones de campo de Einstein que gobiernan la gravedad. El tensor métrico describe la geometría del espacio-tiempo y cómo se curva en presencia de masa y energía.
Los tensores de curvatura describen cómo se curva el espacio-tiempo en presencia de masa y energía. Estos tensores están relacionados con la distribución de masa y energía a través de las ecuaciones de campo de Einstein.
Campos tensoriales
En algunas aplicaciones, los tensores pueden variar en cada punto de un objeto, lo que lleva al concepto de campo tensorial. Un campo tensorial asigna un tensor a cada punto en un espacio. Esto permite describir fenómenos que varían en diferentes regiones del espacio.
Ejemplo de campo tensorial
Un ejemplo común de un campo tensorial es el tensor de esfuerzo en un material sólido, que describe cómo se distribuyen las fuerzas internas en cada punto del material. El tensor de esfuerzo puede variar en cada punto del material, dependiendo de la dirección y magnitud de las fuerzas aplicadas.
Otro ejemplo de campo tensorial es el tensor de curvatura en la relatividad general. Este tensor describe cómo se curva el espacio-tiempo en cada punto del espacio, dependiendo de la distribución de masa y energía en ese punto.
Conclusiones
Un tensor es un objeto algebraico que describe una relación multilineal entre conjuntos de objetos algebraicos relacionados con un espacio vectorial. Los tensores se definen independientemente de cualquier base y se pueden representar como matrices multidimensionales. También se pueden definir como mapas multilineales utilizando productos tensoriales. Los componentes de un tensor se transforman de acuerdo con las leyes de transformación covariantes y contravariantes. Los tensores son importantes en matemáticas y física, y se utilizan para describir una variedad de fenómenos en diferentes áreas de estudio. Comprender los tensores es esencial para abordar problemas complejos en ciencias naturales y aplicadas.