El Teorema de Pitágoras es uno de los conceptos fundamentales de la geometría y se utiliza para calcular la longitud de los lados de un triángulo rectángulo. Fue descubierto por el matemático griego Pitágoras en el siglo VI a.C. y desde entonces ha sido utilizado en numerosas aplicaciones prácticas. Exploraremos en detalle qué es el Teorema de Pitágoras, cómo se aplica y daremos algunos ejemplos para una mejor comprensión.
Definición del Teorema de Pitágoras
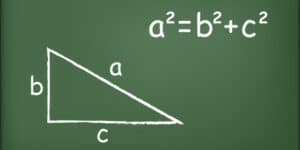
El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los catetos. Matemáticamente, se puede expresar de la siguiente manera:
AB^2 + BC^2 = AC^2
Donde AB y BC son los catetos y AC es la hipotenusa del triángulo rectángulo.
Aplicación del Teorema de Pitágoras
El Teorema de Pitágoras se utiliza para calcular la longitud de uno de los lados de un triángulo rectángulo cuando se conocen los otros dos. También se puede utilizar para verificar si un triángulo es rectángulo si se conocen las longitudes de sus lados.
Cálculo de la longitud de un lado
Para calcular la longitud de un lado de un triángulo rectángulo utilizando el Teorema de Pitágoras, se deben seguir los siguientes pasos:
- Identificar los catetos y la hipotenusa del triángulo rectángulo.
- Asignar valores numéricos a los catetos y/o la hipotenusa.
- Sustituir los valores en la fórmula del Teorema de Pitágoras.
- Resolver la ecuación para encontrar la longitud del lado desconocido.
Por ejemplo, si conocemos que los catetos de un triángulo rectángulo miden 3 y 4 unidades, podemos calcular la longitud de la hipotenusa de la siguiente manera:
3^2 + 4^2 = AC^2
9 + 16 = AC^2
25 = AC^2
AC = √25
AC = 5
Por lo tanto, la longitud de la hipotenusa es 5 unidades.
Verificación de un triángulo rectángulo
Para verificar si un triángulo es rectángulo utilizando el Teorema de Pitágoras, se deben seguir los siguientes pasos:
- Identificar los catetos y la hipotenusa del triángulo.
- Asignar valores numéricos a los catetos y/o la hipotenusa.
- Sustituir los valores en la fórmula del Teorema de Pitágoras.
- Resolver la ecuación.
- Si la ecuación se cumple, el triángulo es rectángulo. Si no se cumple, el triángulo no es rectángulo.
Por ejemplo, si conocemos que los lados de un triángulo miden 5, 12 y 13 unidades, podemos verificar si es un triángulo rectángulo de la siguiente manera:
5^2 + 12^2 = 13^2
25 + 144 = 169
169 = 169
La ecuación se cumple, por lo tanto, el triángulo es rectángulo.
Ejemplos del Teorema de Pitágoras
A continuación, se presentan algunos ejemplos adicionales para una mejor comprensión del Teorema de Pitágoras:
Ejemplo 1
Calcular la longitud de la hipotenusa de un triángulo rectángulo con catetos de longitud 6 y 8 unidades.
Solución:
6^2 + 8^2 = AC^2
36 + 64 = AC^2
100 = AC^2
AC = √100
AC = 10
La longitud de la hipotenusa es 10 unidades.
Ejemplo 2
Verificar si un triángulo con lados de longitud 9, 12 y 15 unidades es rectángulo.
Solución:
9^2 + 12^2 = 15^2
81 + 144 = 225
225 = 225
La ecuación se cumple, por lo tanto, el triángulo es rectángulo.
Conclusiones
El Teorema de Pitágoras es una herramienta fundamental en la geometría y se utiliza para calcular la longitud de los lados de un triángulo rectángulo. También se puede utilizar para verificar si un triángulo es rectángulo. Conocer y comprender este teorema es esencial para resolver problemas geométricos y aplicaciones prácticas en diversos campos.