La topología es una rama de las matemáticas que se enfoca en el estudio de la continuidad y las propiedades de los objetos geométricos que se mantienen sin cambios a través de transformaciones continuas. Es una disciplina fundamental en las matemáticas y tiene aplicaciones en diversos campos, como la física, la ingeniería y la informática. Exploraremos en detalle qué es la topología, cómo se define, sus propiedades y ramas, así como algunos ejemplos concretos.
2. Definición de Topología
La topología se define como el estudio de las propiedades de los espacios que se mantienen invariantes bajo transformaciones continuas. En otras palabras, se ocupa de las propiedades que no cambian cuando se realiza una deformación suave de un objeto. Estas deformaciones pueden incluir estirar, doblar, retorcer o encoger el objeto, siempre y cuando no se rompa ni se segmente.
2.1 Concepto de Topología
El concepto de topología se centra en las funciones continuas y los espacios topológicos. Un espacio topológico es una estructura matemática que permite definir conceptos como la continuidad, la conectividad y la convergencia. Se compone de un conjunto de puntos y una colección de conjuntos llamados abiertos, que satisfacen ciertas propiedades. Estos conjuntos abiertos permiten definir la noción de cercanía y continuidad en el espacio topológico.
La topología se basa en el principio de que las propiedades topológicas son invariantes bajo transformaciones continuas. Esto significa que si dos objetos son topológicamente equivalentes, entonces tienen las mismas propiedades topológicas, independientemente de su forma o tamaño. Por ejemplo, un círculo y un cuadrado son topológicamente equivalentes, ya que ambos tienen una sola componente conexa y no tienen agujeros.
2.2 Propiedades de la Topología
La topología tiene varias propiedades importantes que la distinguen de otras ramas de las matemáticas. Algunas de estas propiedades son:
- Invariancia topológica: Las propiedades topológicas de un objeto no cambian bajo transformaciones continuas. Esto significa que dos objetos topológicamente equivalentes tienen las mismas propiedades topológicas.
- Compacidad: Un espacio topológico es compacto si cada cubierta abierta tiene una subcubierta finita. La compacidad es una propiedad importante en el análisis y la geometría.
- Separabilidad: Un espacio topológico es separable si contiene un subconjunto denso y numerable. Esto significa que el espacio tiene suficientes puntos para aproximarse a cualquier punto dado.
- Conectividad: Un espacio topológico es conexo si no se puede dividir en dos conjuntos disjuntos y abiertos. La conectividad es una propiedad importante en el estudio de las curvas y las superficies.
3. Ramas de la Topología
La topología se divide en varias ramas, cada una de las cuales se enfoca en aspectos específicos de la disciplina. Algunas de las ramas más importantes de la topología son:
- Topología general: Es la rama más básica de la topología y se ocupa del estudio de los espacios topológicos y las funciones continuas.
- Topología diferencial: Se enfoca en el estudio de las variedades diferenciables y las funciones diferenciables. Tiene aplicaciones en la física y la geometría diferencial.
- Topología algebraica: Combina la topología con la teoría de grupos y la teoría de categorías. Se ocupa del estudio de los espacios topológicos desde un punto de vista algebraico.
- Topología combinatoria: Se enfoca en el estudio de las propiedades combinatorias de los espacios topológicos, como los grafos y las redes.
4. Topología de Red
En el ámbito de la informática, la topología de red se refiere a la forma en que los ordenadores se conectan entre sí para el intercambio de información. La topología de red determina cómo se transmiten los datos entre los diferentes nodos de la red.
4.1 Tipos de Topologías de Red
Existen varios tipos de topologías de red, cada una con sus propias ventajas y desventajas. Algunos ejemplos de topologías de red son:
- Topología en estrella: En esta topología, todos los nodos de la red están conectados a un nodo central, como un concentrador o un conmutador. Este nodo central es responsable de gestionar el tráfico de la red.
- Topología en bus: En esta topología, todos los nodos de la red están conectados a un único cable de transmisión. Los datos se transmiten a través de este cable y son recibidos por todos los nodos de la red.
- Topología en anillo: En esta topología, los nodos de la red están conectados en forma de anillo cerrado. Los datos se transmiten en una dirección alrededor del anillo.
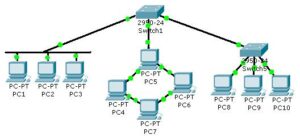
- Topología en árbol: En esta topología, los nodos de la red están organizados en una estructura jerárquica de árbol. Hay un nodo raíz que se conecta a varios nodos secundarios, y cada nodo secundario puede tener sus propios nodos secundarios.
Cada tipo de topología de red tiene sus propias ventajas y desventajas en términos de rendimiento, escalabilidad y confiabilidad. La elección de la topología de red adecuada depende de las necesidades y requisitos específicos de la red.
5. Ejemplos de Topología
La topología se puede aplicar a una amplia variedad de objetos y espacios. A continuación, se presentan algunos ejemplos concretos de topología:
- Espacio euclidiano: El espacio euclidiano es un ejemplo clásico de un espacio topológico. Se compone de puntos en un plano o en el espacio tridimensional, y se puede deformar suavemente sin cambiar sus propiedades topológicas.
- Toro: El toro es otro ejemplo de un espacio topológico. Tiene la forma de un donut y se puede deformar suavemente sin cambiar sus propiedades topológicas.
- Plano proyectivo: El plano proyectivo es un espacio topológico que se obtiene al identificar puntos opuestos en un plano. Tiene la propiedad de que cualquier curva cerrada se puede deformar suavemente en un punto.
Estos ejemplos ilustran cómo la topología permite estudiar las propiedades y características de diferentes objetos y espacios, independientemente de su forma o tamaño.
6. Conclusiones
La topología es una rama fundamental de las matemáticas que se ocupa del estudio de la continuidad y las propiedades de los objetos geométricos que se mantienen sin cambios a través de transformaciones continuas. Se centra en las funciones continuas y los espacios topológicos, que permiten definir conceptos como la continuidad, la conectividad y la convergencia. La topología tiene aplicaciones en diversos campos, como la física, la ingeniería y la informática. Además, existen diferentes ramas de la topología, como la general, la diferencial y la algebraica. En el ámbito de la informática, la topología de red se refiere a la forma en que los ordenadores se conectan entre sí para el intercambio de información, y existen diferentes tipos de topologías de red, como la estrella y el árbol. La topología es una disciplina fascinante que nos permite comprender y analizar las propiedades y características de los objetos y espacios desde una perspectiva matemática.
7. Referencias
1. Munkres, J. R. (2000). Topology (2nd ed.). Prentice Hall.
2. Armstrong, M. A. (1983). Basic Topology. Springer.
3. Hatcher, A. (2002). Algebraic Topology. Cambridge University Press.