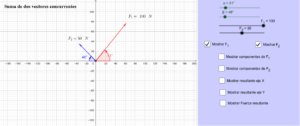
Exploraremos el concepto de vectores concurrentes, que son grupos de vectores cuyos ejes coinciden en un punto. Analizaremos su definición, las diferentes notaciones utilizadas para representarlos y algunos ejemplos comunes en los que se encuentran.
Definición de Vectores Concurrentes
Los vectores concurrentes son grupos de vectores cuyos ejes coinciden en un punto. Esto significa que todos los vectores tienen un punto en común que coincide con su origen. Los vectores concurrentes pueden formar ángulos internos y externos entre ellos.
Notaciones para Representar Vectores Concurrentes
Existen diferentes notaciones utilizadas para representar vectores concurrentes:
- Notación Cartesiana: Los vectores se representan mediante componentes en los ejes x, y y z.
- Notación Polar: Los vectores se representan mediante una magnitud y un ángulo con respecto a un eje de referencia.
- Notación Analítica: Los vectores se representan mediante ecuaciones algebraicas.
- Notación Esférica: Los vectores se representan mediante una magnitud, un ángulo azimutal y un ángulo polar.
La notación cartesiana es la más común y se utiliza en el estudio de vectores en el plano cartesiano. En esta notación, los vectores se representan mediante componentes en los ejes x, y y z. Por ejemplo, un vector en el plano cartesiano puede ser representado como (x, y, z), donde x, y y z son las componentes del vector en los ejes respectivos.
La notación polar se utiliza para representar vectores en coordenadas polares. En esta notación, los vectores se representan mediante una magnitud y un ángulo con respecto a un eje de referencia. Por ejemplo, un vector en coordenadas polares puede ser representado como (r, θ), donde r es la magnitud del vector y θ es el ángulo con respecto al eje de referencia.
La notación analítica se utiliza para representar vectores mediante ecuaciones algebraicas. En esta notación, los vectores se representan mediante ecuaciones que describen su comportamiento. Por ejemplo, un vector puede ser representado como (x(t), y(t), z(t)), donde x(t), y(t) y z(t) son las ecuaciones que describen las componentes del vector en función del tiempo.
La notación esférica se utiliza para representar vectores en coordenadas esféricas. En esta notación, los vectores se representan mediante una magnitud, un ángulo azimutal y un ángulo polar. Por ejemplo, un vector en coordenadas esféricas puede ser representado como (r, θ, φ), donde r es la magnitud del vector, θ es el ángulo azimutal y φ es el ángulo polar.
Operaciones con Vectores Concurrentes
Los vectores concurrentes se utilizan en diversas operaciones, como:
- Suma de Vectores: Se suman las componentes de los vectores para obtener un nuevo vector resultante.
- Diferencia de Vectores: Se restan las componentes de los vectores para obtener un nuevo vector resultante.
- Producto Escalar: Se calcula el producto de las magnitudes de los vectores y el coseno del ángulo entre ellos.
- Producto Vectorial: Se calcula el producto de las magnitudes de los vectores y el seno del ángulo entre ellos.
La suma de vectores es una operación en la que se suman las componentes de los vectores para obtener un nuevo vector resultante. Por ejemplo, si tenemos dos vectores concurrentes A = (2, 3, 4) y B = (1, 2, 3), la suma de estos vectores sería A + B = (3, 5, 7).
La diferencia de vectores es una operación en la que se restan las componentes de los vectores para obtener un nuevo vector resultante. Por ejemplo, si tenemos dos vectores concurrentes A = (2, 3, 4) y B = (1, 2, 3), la diferencia de estos vectores sería A – B = (1, 1, 1).
El producto escalar es una operación en la que se calcula el producto de las magnitudes de los vectores y el coseno del ángulo entre ellos. El resultado es un número escalar. Por ejemplo, si tenemos dos vectores concurrentes A = (2, 3, 4) y B = (1, 2, 3), el producto escalar de estos vectores sería A · B = 2*1 + 3*2 + 4*3 = 2 + 6 + 12 = 20.
El producto vectorial es una operación en la que se calcula el producto de las magnitudes de los vectores y el seno del ángulo entre ellos. El resultado es un nuevo vector perpendicular a los vectores originales. Por ejemplo, si tenemos dos vectores concurrentes A = (2, 3, 4) y B = (1, 2, 3), el producto vectorial de estos vectores sería A x B = (3*3 – 2*4, 4*1 – 2*3, 2*2 – 3*1) = (1, -2, 1).
Ejemplos de Vectores Concurrentes
Los vectores concurrentes se encuentran en diversas situaciones y aplicaciones. Algunos ejemplos comunes incluyen:
- Fuerzas que actúan sobre un objeto: Las fuerzas que actúan sobre un objeto pueden ser representadas como vectores concurrentes. Por ejemplo, si un objeto está siendo empujado hacia arriba por una fuerza de 10 N y hacia abajo por una fuerza de 5 N, los vectores que representan estas fuerzas serían F1 = (0, 10, 0) y F2 = (0, -5, 0).
- Velocidades relativas de dos objetos: Las velocidades relativas de dos objetos en movimiento pueden ser representadas como vectores concurrentes. Por ejemplo, si un objeto se mueve hacia el este a una velocidad de 5 m/s y otro objeto se mueve hacia el oeste a una velocidad de 3 m/s, los vectores que representan estas velocidades serían V1 = (5, 0, 0) y V2 = (-3, 0, 0).
- Aceleraciones relativas de dos objetos: Las aceleraciones relativas de dos objetos en movimiento pueden ser representadas como vectores concurrentes. Por ejemplo, si un objeto está acelerando hacia arriba a una aceleración de 2 m/s^2 y otro objeto está acelerando hacia abajo a una aceleración de 1 m/s^2, los vectores que representan estas aceleraciones serían A1 = (0, 2, 0) y A2 = (0, -1, 0).
Conclusiones
Los vectores concurrentes son grupos de vectores cuyos ejes coinciden en un punto. Se representan mediante diferentes notaciones y se utilizan en operaciones como la suma, diferencia, producto escalar y producto vectorial. Son comunes en el estudio de vectores y tienen aplicaciones en diversas ramas de la ciencia. Algunos ejemplos de vectores concurrentes son las fuerzas que actúan sobre un objeto, las velocidades relativas de dos objetos y las aceleraciones relativas de dos objetos.