Definición de aceleración angular
La aceleración angular es la alteración que se registra en la velocidad angular en un determinado periodo de tiempo. La velocidad angular mide, por unidad de tiempo, el ángulo girado por un elemento que realiza un movimiento de rotación. La aceleración angular está vinculada a cómo cambia la velocidad alcanzada por un elemento que gira en un movimiento de rotación. Se expresa en radianes por segundo al cuadrado y se representa con la letra alfa del alfabeto griego. Tanto la aceleración angular como la velocidad angular son magnitudes vectoriales.
La aceleración angular es una medida de cómo cambia la velocidad angular de un objeto en movimiento circular. En otras palabras, es la tasa de cambio de la velocidad angular en relación con el tiempo. Si un objeto está girando a una velocidad constante, su aceleración angular será cero, ya que no hay cambios en la velocidad angular. Sin embargo, si el objeto está acelerando o desacelerando en su movimiento circular, su aceleración angular será diferente de cero.
La aceleración angular es una cantidad vectorial, lo que significa que tiene magnitud y dirección. La magnitud de la aceleración angular se mide en radianes por segundo al cuadrado y representa la rapidez con la que cambia la velocidad angular. La dirección de la aceleración angular está determinada por la dirección en la que cambia la velocidad angular. Si la velocidad angular está aumentando, la aceleración angular apunta en la misma dirección que la velocidad angular. Si la velocidad angular está disminuyendo, la aceleración angular apunta en dirección opuesta a la velocidad angular.
Cálculo de la aceleración angular
1. Calcular la aceleración angular promedio
Para calcular la aceleración angular promedio, se deben medir la velocidad angular inicial, la velocidad angular final y el tiempo transcurrido. La fórmula para calcular la aceleración angular promedio es:
aceleración angular promedio (α promedio) = (velocidad angular final – velocidad angular inicial) / tiempo transcurrido
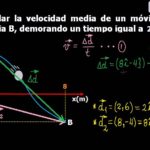Aceleración MediaPor ejemplo, si un objeto comienza a girar con una velocidad angular de 2 radianes por segundo y después de 5 segundos alcanza una velocidad angular de 8 radianes por segundo, la aceleración angular promedio sería:
α promedio = (8 rad/s – 2 rad/s) / 5 s = 1.2 rad/s²
Esto significa que la velocidad angular del objeto está aumentando a una tasa de 1.2 radianes por segundo al cuadrado durante ese periodo de tiempo.
2. Calcular la aceleración angular instantánea
Para calcular la aceleración angular instantánea, se debe determinar la posición de la función angular, buscar la función de la velocidad angular, encontrar la función de la aceleración y aplicar los datos para encontrar la aceleración instantánea.
La aceleración angular instantánea se calcula utilizando cálculo diferencial. Se encuentra la derivada de la función de la velocidad angular con respecto al tiempo para obtener la función de la aceleración angular. Luego, se evalúa la función de la aceleración angular en un punto específico para obtener la aceleración angular instantánea en ese punto.
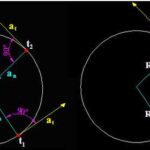Aceleración TangencialPor ejemplo, si la función de la velocidad angular es ω(t) = 3t² + 2t + 1, se encuentra la derivada de esta función para obtener la función de la aceleración angular:
α(t) = dω(t)/dt = 6t + 2
Si se evalúa la función de la aceleración angular en t = 2 segundos, se obtiene la aceleración angular instantánea en ese punto:
α(2) = 6(2) + 2 = 14 rad/s²
Esto significa que en ese punto específico, la velocidad angular está aumentando a una tasa de 14 radianes por segundo al cuadrado.
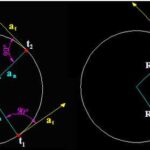Aceleración Centrífuga3. Medir el movimiento angular en radianes
Para revisar la aceleración angular, se puede medir el movimiento angular en radianes. Esto implica medir el ángulo girado por el objeto en movimiento circular y utilizar esa medida para calcular la aceleración angular.
Por ejemplo, si un objeto gira 3 vueltas completas en 10 segundos, se puede calcular la aceleración angular utilizando la fórmula:
α = (2πθ) / t²
Donde θ es el ángulo girado en radianes y t es el tiempo transcurrido. Si se convierten las 3 vueltas completas a radianes (1 vuelta = 2π radianes), se obtiene:
θ = 3(2π) = 6π radianes
Si se sustituyen los valores en la fórmula, se obtiene:
α = (2π(6π)) / (10²) = 3.6 rad/s²
Esto significa que la aceleración angular del objeto es de 3.6 radianes por segundo al cuadrado.
Aceleración angular en diferentes tipos de movimiento circular
En un movimiento circular uniforme (MCU), donde la velocidad angular es constante, la aceleración angular es igual a cero. Esto se debe a que no hay cambios en la velocidad angular a lo largo del tiempo. En un MCU, el objeto gira a una velocidad constante y no acelera ni desacelera.
Por ejemplo, si un objeto está girando a una velocidad angular constante de 4 radianes por segundo, su aceleración angular será cero, ya que no hay cambios en la velocidad angular.
En un movimiento circular uniformemente acelerado (MCUA), donde la aceleración angular se mantiene constante, se registra una aceleración angular. Esto se debe a que la velocidad angular está cambiando constantemente a medida que el objeto acelera o desacelera en su movimiento circular.
Por ejemplo, si un objeto comienza a girar con una velocidad angular de 2 radianes por segundo y su aceleración angular es de 3 radianes por segundo al cuadrado, su velocidad angular aumentará a medida que el tiempo avanza. Después de un cierto periodo de tiempo, la velocidad angular del objeto será mayor que 2 radianes por segundo.
La aceleración angular es una medida de cómo cambia la velocidad angular de un objeto en movimiento circular. Se puede calcular utilizando diferentes métodos, como el cálculo de la aceleración angular promedio, el cálculo de la aceleración angular instantánea y la medición del movimiento angular en radianes. La aceleración angular puede ser cero en un movimiento circular uniforme y diferente de cero en un movimiento circular uniformemente acelerado.