Ángulos Suplementarios

Exploraremos en detalle la definición de los ángulos suplementarios, su importancia en la geometría y su aplicación en diferentes áreas. También veremos ejemplos de cómo identificar y calcular ángulos suplementarios.

Los ángulos suplementarios son figuras geométricas formadas por dos semirrectas que suman 180 grados. Son fundamentales en disciplinas como las matemáticas y la arquitectura, y se utilizan para resolver problemas de geometría y calcular áreas y perímetros de figuras. También son importantes en el diseño y construcción de estructuras estables y resistentes.

¿Qué son los ángulos suplementarios?

Los ángulos suplementarios son aquellos ángulos que, cuando se suman entre sí, dan como resultado dos ángulos rectos, es decir, 180 grados. Estos ángulos están formados por dos semirrectas que comparten un origen o vértice.

Características de los ángulos suplementarios

• La suma de los ángulos suplementarios es siempre igual a 180 grados.
• Los ángulos suplementarios pueden estar formados por dos ángulos agudos, dos ángulos obtusos o un ángulo agudo y un ángulo obtuso.
• Los ángulos suplementarios pueden ser adyacentes si comparten un lado y sus otros dos lados son semirrectas opuestas, o consecutivos si tienen un lado y el vértice en común.

Diferencia entre ángulos suplementarios y ángulos complementarios

Es importante no confundir los ángulos suplementarios con los ángulos complementarios. Mientras que los ángulos suplementarios suman 180 grados, los ángulos complementarios suman 90 grados.

Aplicaciones de los ángulos suplementarios

Los ángulos suplementarios se encuentran en diversas estructuras que soportan mucho peso, como puentes de arcos, carpas y vigas perpendiculares al suelo. Estos ángulos permiten distribuir la carga de manera equilibrada y garantizar la estabilidad de las estructuras.

Lee TambiénÁlgebra Booleana

En matemáticas

Los ángulos suplementarios son fundamentales en la geometría y el cálculo. Se utilizan para resolver problemas de trigonometría, calcular áreas y perímetros de figuras geométricas, y determinar relaciones entre ángulos y lados en triángulos y polígonos.

En arquitectura

Los ángulos suplementarios son utilizados en el diseño y construcción de edificios y estructuras arquitectónicas. Ayudan a determinar la ubicación y orientación de las paredes, ventanas y puertas, y garantizan la estabilidad y resistencia de las estructuras.

Cómo identificar y calcular ángulos suplementarios

Para identificar si dos ángulos son suplementarios, debemos sumar sus medidas y verificar si el resultado es igual a 180 grados. Si es así, los ángulos son suplementarios.

Para calcular un ángulo suplementario a partir de otro ángulo dado, podemos restar la medida del ángulo dado a 180 grados. El resultado será la medida del ángulo suplementario.

Ejemplo 1

Si tenemos un ángulo de 120 grados, podemos calcular su ángulo suplementario de la siguiente manera:

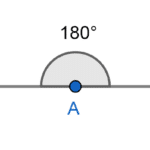Lee TambiénÁngulo Llano

Ángulo suplementario = 180 grados - 120 grados = 60 grados

Ejemplo 2

Si tenemos un ángulo de 30 grados, podemos calcular su ángulo suplementario de la siguiente manera:

Ángulo suplementario = 180 grados - 30 grados = 150 grados

Conclusión

Los ángulos suplementarios son figuras geométricas formadas por dos semirrectas que suman 180 grados. Son importantes en disciplinas como las matemáticas y la arquitectura, y se utilizan para resolver problemas de geometría y calcular áreas y perímetros de figuras. También son fundamentales en el diseño y construcción de estructuras estables y resistentes.